热身赛光荣打铁，只能回来补题。。

思路

题目来源Kickstart Round A 2017 Problem A。大致意思是从一个m*n矩形中能选出多少个正方形（这里给的是点数，我们默认m-1,n-1）。对于这个问题我们把斜着的正方形和正常的正方形分开考虑。
对于正常的正方形有：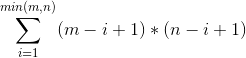

对于斜着的正方形有：（画张图考虑后能发现斜着且撑满的正方形只有k-1个，然后从小正方形到大正方形累加）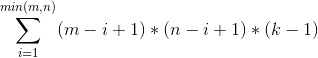

化简可得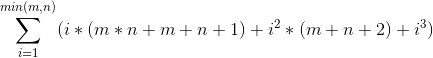

利用平方和公式和立方和公式我们能O(1)求出答案

思路

模板题，保存DFS序后使用RMQ求LCA。这个算法相对来说比较好理解。我们访问的顺序是类似根-子节点-根的顺序，记录访问顺序后使用RMQ查询两点之间depth的最小值就是LCA。这题我真的是无限RE,最后发现是自己ST表的模板有问题。。

思路

题意是一个人要参加不同的晚会需要穿不同的衣服，衣服可以意见套一件然后再反序脱掉，问最少需要多少件衣服。容易想到使用区间dp。一开始想的状态转移方程是当两端不匹配时，dp[l][r]=min(dp[l+1][r],dp[l][r-1])+1。当两端匹配时，dp[l][r]=dp[l+1][r-1]+1。一开始还觉得没问题，结果得了WA。发现不能只考虑两端的复用，要考虑第一件衣服和中间某件（假设为k）的复用，因为有可能在中间复用会使得dp[l][r]更小。
状态转移方程:
对于两端不匹配的情况:dp[l][r]=min(dp[l+1][r],dp[l][r-1])+1;
对于l-r范围中我们枚举k，如果cloth[l]==cloth[k]，代表我们考虑中间第k件复用:dp[l][r]=min(dp[l][r],dp[l][k-1]+dp[k+1][r]);

思路

一道非常好的kmp题。如果我们想要使用kmp的话，模式串一定要是固定的才行，而本题中，我们是要找一个排名串。这一就要用到一个结论：两个排名串相等，当且仅当对于两个排名串其中相同位置的数，他俩之前比他俩小的数字个数相等而且小于等于他俩的数字个数也相等。这样就转化为了固定的模式串的问题。然后我们需要修改makenext这个函数和kmp的匹配函数，因为其中有动态的增加减少，比如我们失配的时候，我们需要减掉一部分不必要的数字前缀（见代码）。为了取得比一个数小的个数和小于等于他的数，我们使用树状数组（也可以枚举）。题意给了数字最大不超过30，我们开一个BIT[30],然后维护这个树状数组。最后的问题就是POJ的g++似乎对cin，cout很不友好啊？我用c++得了ac，用g++居然TLE???真是玄学。

思路

莫队算法

莫队算法是一种解决一系列无修改的区间查询问题的算法。对于区间查询问题，我们通常使用线段树。但是考虑这样一个问题：对[l,r]区间内的计算至少重复三次数的个数。这样的问题如果使用线段树需要在节点上维护区间内数字的个数，而这样维护显然并不能在O(1)完成，因而我们常常使用莫队算法。莫队算法的使用条件是我们可以O(1)时间内通过已知的[l,r]答案得到[l-1,r],[l+1,r],[l,r+1],[l,r-1]的答案，并且我们能够离线询问。通过对询问排序，我们利用O(1)的转移能够以一个较为满意的复杂度解决这个问题(避免重复扫描数列）。这个问题可以使用曼哈顿距离最小生成树来写，但这样写代码似乎太麻烦了些，所以我们使用分块。我们以询问左端点所在的分块的序号为第一关键字，右端点的大小为第二关键字。

莫队算法时间复杂度

分块相同时，右端点递增是O(N)的，分块共有O(sqrt(N)) )个，复杂度为O(N^(1.5))
分块转移时，右端点最多变化N，分块共有O(sqrt(N) )个，复杂度为O(N^(1.5)
分块相同时，左端点最多变化sqrt(N) ，分块转移时，左端点最多变化2sqrt(N) ，共有N个询问，复杂度为O(N^(1.5) )
所有总时间复杂度就是O(N^1.5)

参考

莫队算法 (Mo’s Algorithm)
莫队算法

本题思路

莫队模板题。令当前可选的袜子为ans
ans=(color[i]*(color[i]-1)/2);
化简得到ans=(Σ(sum(color[i])2)−(R−L+1))/((R−L+1)∗(R−L))
所以更新为ans=ans-ci^2+(ci+1)^2

思路

本题是后缀数组一个常见的应用，不可重叠最长重复子串。后缀数组的基本知识参考SPOJ - SUBST1 New Distinct Substrings一文。对于一个不可重叠最长子串的问题，我们首先对长度二分答案，然后对height数组分段，连续的height值>=k的我们分在一起，然后记录段内sa的最小值和最大值，如果两者的差大于等于k+1（题意要求重复子串之间要有一个字符的间隔）那么现在的k就是符合条件的。需要注意的是这道题卡了cin,cout。

思路

在有根树中，我们称距离u和v所有公共祖先中距离最近的称为最近公共祖先(LCA)。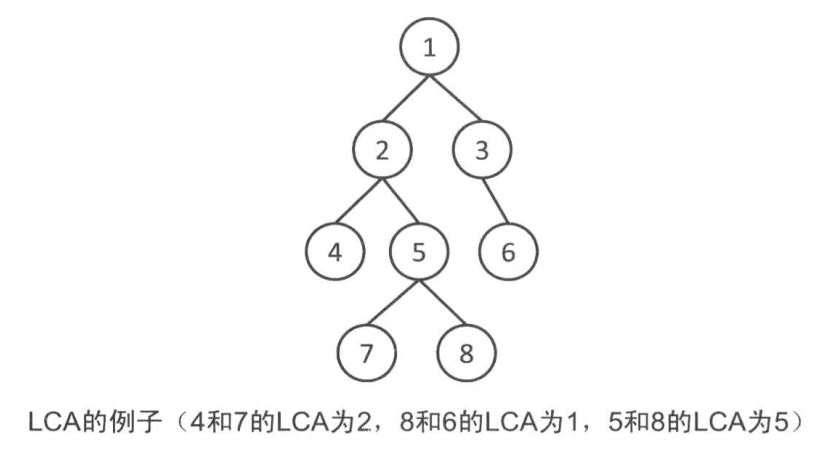

一个朴素的求u和v的LCA的想法是让u和v先深度相同，然后逐层向上直到碰到相同元素。复杂度为O(n)。虽然看着简单有效，但对多次查询来说这个复杂度十分不友好。
为了高效求解公共祖先，我们有三种方式：

• 倍增法（在线，实现简单）
• RMQ（在线，实现复杂）
• Tarjan（离线）

本题我们使用倍增法求LCA。倍增法构造LCA预处理复杂度为O(nlogn),查询复杂度为O(logn)。
下面会涉及到的一些元素：

• parent[k][v]:距离v元素2^k距离的祖先
• depth[v]:v元素的深度

我们首先通过dfs(int v,int p,int d)初始化parent[0][v],depth[v],根的祖先为-1

1
2
3
4
5
6
7

void dfs(int v, int p, int d) {
	parents[0][v] = p;
	depth[v] = d;
	for (vector<int>::iterator it = G[v].begin();it != G[v].end();it++) {
		if(*it!=p)dfs(*it, v, d + 1);
	}
}

1
2
3
4
5
6
7
8
9

void init() {
	dfs(root, -1, 0);
	for (int k = 0;k + 1 < MAX_LOG_V;k++) {
		for (int v = 1;v <= n;v++) {
			if (parents[k][v] < 0)parents[k + 1][v] = -1;
			else parents[k + 1][v] = parents[k][parents[k][v]];
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

int lca(int u, int v) {
	if (depth[u] > depth[v])swap(u, v);
	for (int k = 0;k < MAX_LOG_V;k++) {
		if (((depth[v] - depth[u]) >> k) & 1) {
			v = parents[k][v];
		}
	}
	if (u == v)return u;
	for (int k = MAX_LOG_V - 1;k >= 0;k--) {
		if (parents[k][u] != parents[k][v]) {
			u = parents[k][u];
			v = parents[k][v];
		}
	}
	return parents[0][u];
}

目录

• A.Div. 64(implementation)
• B.Cubes for Masha(brute force)
• C.Solution for Cube(brute force, implementation)
• D.Ratings and Reality Shows(data structures, two pointers)
• E.Little Brother(binary search, geometry)
• F.Row of Models

思路

最小瓶颈路

给定两个点u,v求两点间路径上最大边权最小，这就是最小瓶颈路问题。

解法

对于最小瓶颈路，我们通常有两种解法：

1. Floyd
   通过将原先dp[i][j]=max(dp[i][j],dp[i][k]+dp[k][j])改为dp[i][j]=min(dp[i][j],max(dp[i][k],dp[k][j]))来计算，复杂度O(n^3)
2. 最小生成树
   通过观察Kruskal算法的过程我们显然能够发现最小瓶颈路在最小生成树上。对于单点查询dfs就可解决问题。如果多次查询可以使用类似Floyd的处理。对于本题，我们可以离线询问，然后每次判断询问的两点是否已经相连，如果相连那么现在加入的边就是我们要求的边。

   代码

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123

   #include <iostream> #include <iomanip> #include <cstdio> #include <cstdlib> #include <cstring> #include <string> #include <algorithm> #include <cmath> #include <queue> #include <vector> #include <map> #include <set> #include <stack> #include <cctype> #include <sstream> #define INF 1e9 #define ll long long #define ull unsigned long long #define ms(a,val) memset(a,val,sizeof(a)) #define lowbit(x) ((x)&(-x)) #define lson(x) (x<<1) #define rson(x) (x<<1+1) using namespace std; int c, s, q; int fa[105], ranks[105]; struct edge { int u, v, val; edge() {}; edge(int u, int v, int val) :u(u), v(v), val(val) {}; }E[1005]; //vector<pair<int,int>> G[105]; vector<pair<int, int>> qu; map<pair<int, int>, int> dict; bool cmp(edge e1, edge e2) { return e1.val < e2.val; } void init_union() { for (int i = 0;i <= c;i++) { fa[i] = i, ranks[i] = 0; } } int getfa(int x){ if (fa[x] == x)return x; else return fa[x] = getfa(fa[x]); } bool same(int i, int j) { return getfa(i) == getfa(j); } void unite(int i,int j) { int a = getfa(i), b = getfa(j); if (a == b)return; else { if (ranks[a] < ranks[b]) { fa[a] = b; } else { fa[b] = a; if (ranks[a] == ranks[b])ranks[a]++; } } } int kruskal() { init_union(); int ans = 0; sort(E, E + s, cmp); for (int i = 0;i < s;i++) { if (!same(E[i].u, E[i].v)) { ans += E[i].val; unite(E[i].u, E[i].v); //G[E[i].u].push_back(make_pair(E[i].v, E[i].val)), G[E[i].v].push_back(make_pair(E[i].u, E[i].val)); for (map<pair<int, int>, int>::iterator it = dict.begin();it != dict.end();it++) { int fi = it->first.first, se = it->first.second; if (same(fi, se) && !it->second)it->second = E[i].val; } } } return ans; } /*void dfs(int index) { vis[index] = 1; for (vector<pair<int,int>>::iterator it = G[index].begin();it != G[index].end();it++) { int to = it->first; if (!vis[to]) { for (int i = 1;i <= c;i++) { if (vis[i]) { dp[i][to] = dp[to][i] = max(dp[i][index], it->second); } } dfs(to); } } }*/ int main() { ios::sync_with_stdio(false), cin.tie(0), cout.tie(0); int u, v, val,cal=0; while (cin >> c >> s >> q) { if (c == 0 && s == 0 && q == 0)break; int i; for (int i = 0;i < s;i++) { cin >> u >> v >> val; edge e(u, v, val); E[i] = e; } for (int i = 0;i < q;i++) { cin >> u >> v; qu.push_back(make_pair(u, v)); dict[make_pair(u, v)] = 0; } kruskal(); if (cal)cout << "\n"; cout << "Case #" << cal + 1 << "\n"; for (vector<pair<int, int>>::iterator it = qu.begin();it != qu.end();it++) { int ans = dict[*it]; if (!ans)cout << "no path\n"; else cout << ans << "\n"; } cal++; qu.clear(),dict.clear(); } return 0; }

思路

题意是计算字符串所有本质不同的子串。主要思路是利用后缀数组的性质。因为是第一次使用后缀数组，所以在这里稍微做一些笔记。

后缀数组

后缀指的是从字符串的某个位置到字符串结尾的子串（包括原串和空串）。而后缀数组指的是包括所有字符串后缀的一个数组，同时其中的后缀已经完成了字典序的排序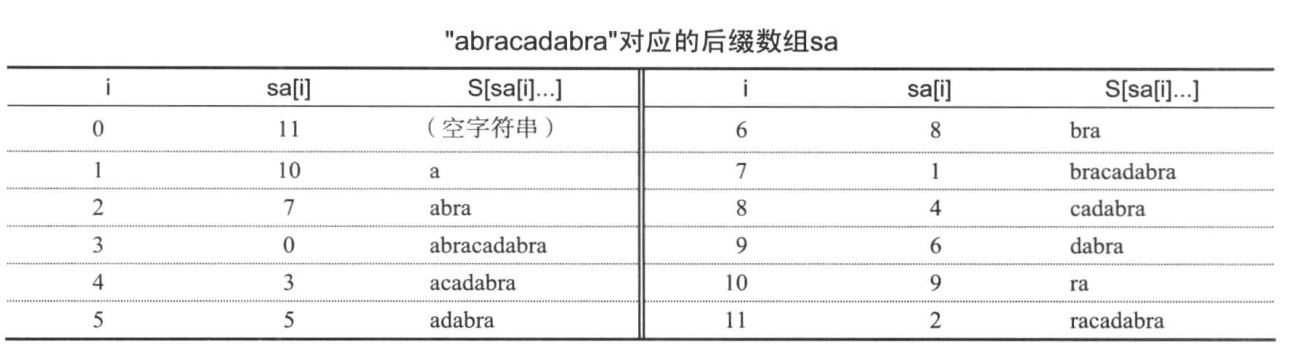

上图就是白书中后缀数组的样例，其中sa[i]指的是从第几个字符开始的后缀。

后缀数组的生成

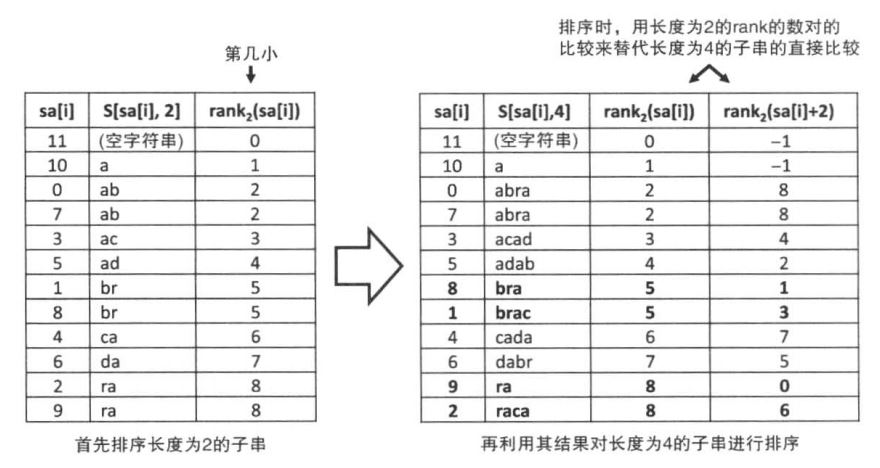
在了解了后缀数组的内容后我们首先来讲讲如何实现。后缀数组的实现类似于基数排序，先比较各个后缀的第一个字符，然后利用这次的比较结果，我们能够计算长度为2的rank（先比较前一个长度为一的字符串，在比较后一个）。通过不断倍增长度最后完成对所有长度字符串的排序，如果发现后半部分长度超过字符串长度的话，就令他为最小的（-1）,可以参考下面第二张图的a的第二个rank。这里或许会不能理解为什么可以这样比，难道不会有遗漏的字符使得这样的比较不能够进行吗？答案是否定的。实际上每一个后缀的第一个字符拼在一起就是整个字符串，所以不用担心有缺漏的情况。这个过程的时间复杂度为O(nlog^2n)。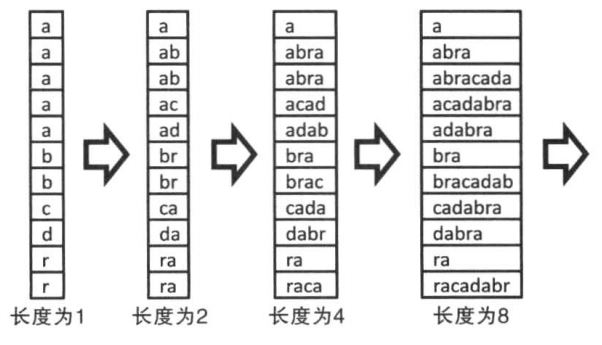

高度数组

高度数组指的是相邻两个后缀的公共最长前缀。

在高度数组中，最关键的就是height[i] ≥ height[i - 1] - 1这个性质。i与i-1指的是sa中相邻的两个后缀，比如abra和bra，从上图中我们能够看到abra后面三个子串和bra后面三个子串只是差一个前面的a，那么我们就能复用之前abra的height数组，所以显然有height[i] ≥ height[i - 1] - 1，构造的时间复杂度为O(n)。

本题思路

在了解了后缀数组的性质后，我们可以发现，一个后缀对子串数量的贡献是str.length()-sa[i]-height[i]。原理是height就是重复的子串，减掉就是去重的过程。