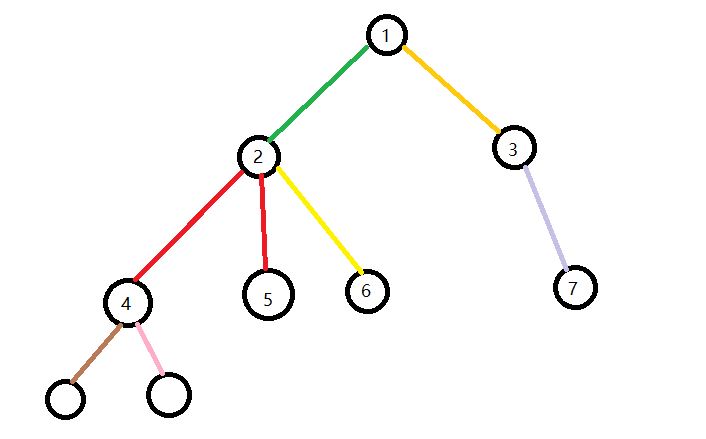
题意可得我们要求一个网络流的最小割。但由于dinic时间复杂度是O(EV^2)，显然对于这张图来说边数会达到10^6以上，所以dinic的时间复杂度是不满足我们的要求的。所以我们学习一个O(nlogn)的姿势——网络流最小割转对偶图最短路。对偶图的概念摸这里。通过观察我们能发现对偶图中的环即对应着原图的割，但直接用对偶图环的性质我们并没有什么高效的算法。所以我们在建图过程中稍作修改，我们这样对样例建图：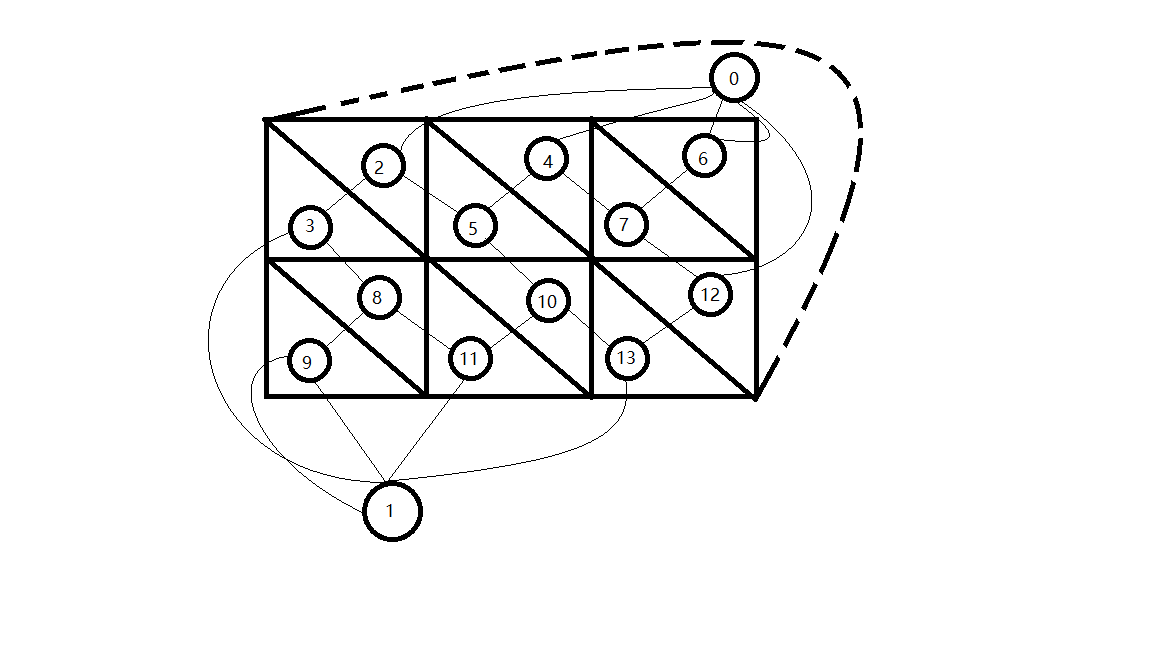
我们先在左上角的源点和右下角的汇点连一条线，如上图，然后再建对偶图。这时比较对偶图的性质显然可以知道对偶图中0到1的最短路即为最小割，运用spfa或dijkstra堆优化就能做到O(nlogn)。
本题我们定义dp[i][j]为队伍中有i个人Tomato排在第j个时，服务器崩溃且排在他前面的人有大于等于k个人的概率。
一共有三个转移方程（注意是逆推）：
接下来我们发现这个dp转移方程。。构成了一个环？不过这道题并没有用到高斯消元，我们将dp转移中第j项与dp[i]即当前状态无关的令为一个常数c[j]，然后对第一个方程迭代。我们最后化简可得如下式子：
然后我们用转移方程求出所有dp[i]的状态，然后dp[n][m]就是答案。这题有个比较奇怪的点，似乎如果不对p4约等于0的情况进行特判会出问题？不是很懂为什么。。
第一反应是最长公共子序列乱搞。。显然不对啊
我们令dp[i][j]为从s1(1,i)转换到s2(1,j)所需要的最少步数。分四种情况讨论:
最后打印路径即可，因为这里操作可逆
对于一个点，考虑可能出现同色边的情况，可以分为两种
(1)两个儿子是相同颜色的
如上图，显然2-4，2-5边是相同颜色的，同时对于4，5节点的子树上的点都不是good的，因为显然会有一条从5（4）到该点的一条不是rainbow road的路径。所以我们需要对这样的子树进行染色。
(2)父亲和儿子是相同颜色的
这种情况下我们需要将除2和2的子树以外的所有节点进行染色。因为他们总有一条过1-2-5非彩虹路，所以那些节点不是good的。
现在我们解决了如何找出非good点这个问题，但是统计依然是大问题。我们需要对子树进行染色。我们注意到我们只需要最后输出一次答案即可而不需要一直回答询问，所以我们可以考虑树上差分。我们首先求出一个dfs序，得到st[i]和ed[i],对于第一种情况，因为st[i]和ed[i]之间的节点就是i和i的子树，我们使用差分即可。对于第二种情况，我们在根上+1，然后在子树上抵消这个+1即可。
概率/期望dp。本题我们能通过全期望公式得到dp[i][j]=dp[i+1][j]*map[i][j][2]+dp[i][j+1]*map[i][j][1]+dp[i][j]*map[i][j][0]+2得到(2是消耗的能量）。由于dp要求无后效性，我们移项得到dp[i][j]=(dp[i+1][j]*map[i][j][2]+dp[i][j+1]*map[i][j][1]+2)/(1-map[i][j][0])。需要注意的是对于概率dp，我们通常正推，但期望dp我们通常反着推。就期望dp来说，正推最大的困难点在于一个点可能是直接转移过来的，但也有可能在原地停留后再转移，即转移概率需要另外计算，所以概率并不是简单的map[i][j][k]。对于本题来说正推计算后的公式实际上还能接受，但对像hdu4405这种题来说正推的转移太复杂了，所以我们考虑泛用性更好的反推。对于一个点X，显然有如下转移
那我们显然地，通过这个转移从起点到终点的期望等于使用这个转移从终点到起点的期望。对于这个反推我们考虑从右下往左上推，注意，这个时候每个点的期望是从右边的点，下面的点和自己推来的，这意味着原来正推的时候该点左下角的点对该点下面的点的影响是没有的，所以可以放心的使用全期望公式。
总结一下，我们使用反推通常是因为我们可以很方便地知道一个点到下一个点的转移概率，这个概率在反推的时候是不用额外计算的。但正推就要考虑之前的点有没有通过多种方式转移到这个点，我们需要考虑转移的概率究竟是几。两相比较之下显然反推比较优秀。