题意

给定一个数组，问需要多少次两个元素的交换操作后使得数组中只有一个逆序对

解法

首先考虑使用交换操作使数组排序需要多少次。有个显而易见的结论是，如果我们将每个元素指向自己本身指向的位置,如下图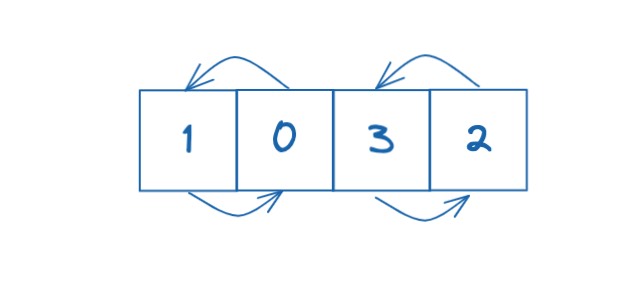

那么显然，这样的边会恰好连成一个环。而环中所有的元素复位，只需要环的大小-1次操作。对于整个数组来说，这个次数是

$\sum_{i=1}^{k}(circlesize-1)$

将k个环size相加为n，所以可以化简得到（k是环的个数）

$n-k$

在解决了使用交换操作使数组排序需要多少次后，我们来看我们现在手上的这个问题。我们来观察只有一个逆序对的数组是什么样的：

2 1 3 4 5…

1 3 2 4 5…

1 2 4 3 5…

显然这些数组都有一个显著的特点即是排序的数组对相邻的两个元素进行反转。那么参考排序的方法，我们将相邻两个元素，假定原先是i位置指向x,i+1指向y，改成i位置指向y，i+1指向x，再跑原来的方法，就可以得到只有一个逆序对的数组了。但是这种方法需要遍历所有相邻元素跑我们的算法，时间复杂度是O(n^2)。实际上我们可以先跑一遍排序算法，然后对每个数组元素染色。我们可以发现，这种交叉操作后，如果两个相邻元素原本是同一个环，那么交换后环就会+1。反之，环会-1.具体实现可以参考Codeforce中的评论，这个评论的图我认为已经非常直观了。这样就避免了一个一个交换再O(n)判断环的个数这种麻烦操作。所以最后总结一下思路就是：

跑最少交换排序算法，获得环的个数
遍历数组，观察是否有相邻元素在相同的环，是则答案变成n-(k+1
)，否则答案是n-(k-1)

代码

#include <bits/stdc++.h>

using namespace std;
using ll = long long;

void solve() {
    int n;
    cin>>n;
    vector<int> nums(n);
    for(int i = 0; i < n; i++) {
        cin>>nums[i];
    }
    vector<int> vis(n, -1);
    int cnt = 0;
    for(int i = 0; i < n; i++) {
        if(vis[i]!=-1) {
            continue;
        }
        cnt++;
        int j = i;
        while(vis[j]==-1) {
            vis[j] = i;
            j = nums[j]-1;
        }
    }
    int flag = -1;
    for(int i = 0; i < n-1; i++) {
        if(vis[i]==vis[i+1]) {
            flag = 1;
        }
    }
    cout<<n-cnt-flag<<endl;
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("./input.txt","r",stdin);
    freopen("./output.txt","w",stdout);
#endif // ONLINE_JUDGE
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int T=1;
    cin>>T;
    while(T--) {
      solve();
    }
    return 0;
}