Edu round 135 tutorial
A. Colored Balls: Revisited
Problem Description
There are n balls with different color in a bag. You can take out two balls with differnt color at a time. We want to know the color of remaining balls.
Solution
You can always find a way to pick up balls that make the color with the largest count have the last ball. I’ve solved a problem on leetcode that find out how many balls can you pick out given the count of balls with different color, which is similar to this problem. To make it as large as possible, the best solution is to first sort the count, then connect balls in i to i+1. If there is still many balls in the last pile, then break the connection before into 2 balls, and connect these two balls with the balls in the last pile. Through this solution, you can find that we can always make the last ball in the last pile.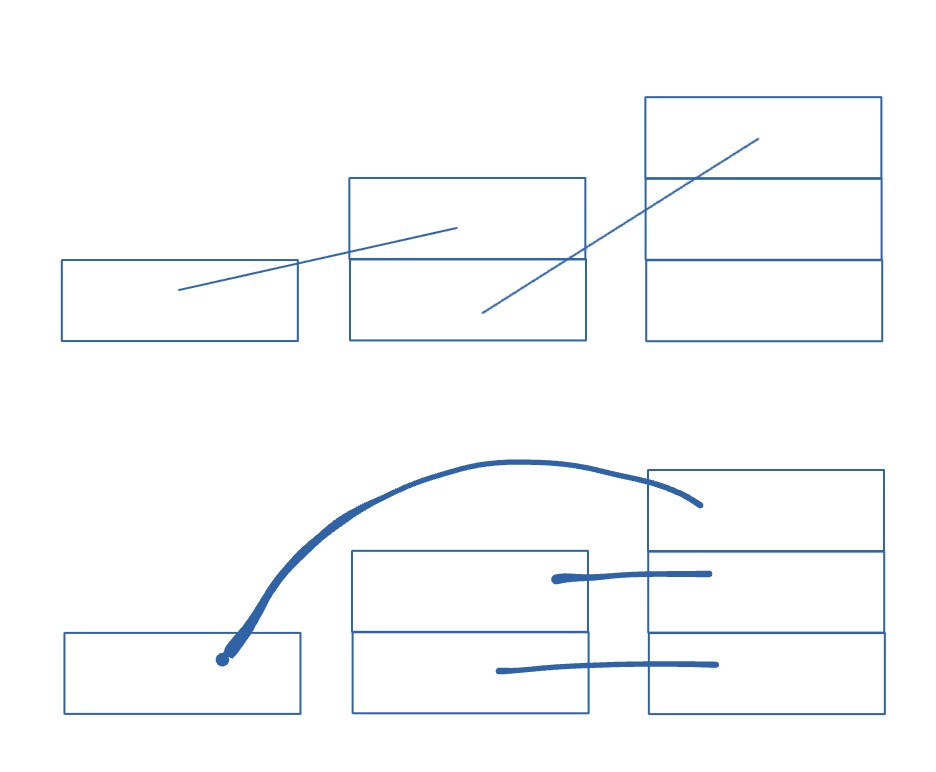
Code
1 |
|
B. Best Permutation
Problem Description
You are asked to generate a permutation that following the rules and have the maximum value. The rule is:
- We have a variable x with value 0.
- Beginning from position 0, if permutation position’s value is larger than x, then x = 0. Else x = x+permutation position’s value.
Solution
The maximum number must be 2n+1. Consider a sequence i, i+1, i+2. It’s obvious that x will be 2i+1, which must be larger than i+2 and become 0. So the best choice is to put n-1, n at the tail of the sequence. Then we want to make x at position at n-2 equal to zero. A decreasing sequence meet the demands when the length is even. For odd, we place the last 3 numbers before n-1, {1, 2, 3} to meet the demands.Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
using namespace std;
using ll = long long;
void solve() {
int n;
cin>>n;
vector<int> ans(n);
if(n%2==0){
for(int i = 0; i < n-2; i++) {
ans[i] = n-2-i;
}
ans[n-2] = n-1, ans[n-1] = n;
for(int i = 0; i < n; i++) {
cout<<ans[i]<<" \n"[i==n-1];
}
} else {
for(int i = 0; i < n-5; i++) {
ans[i] = n-2-i;
}
ans[n-5] = 1, ans[n-4] = 2, ans[n-3] = 3;
ans[n-2] = n-1, ans[n-1] = n;
for(int i = 0; i < n; i++) {
cout<<ans[i]<<" \n"[i==n-1];
}
}
}
int main(){
freopen("./input.txt","r",stdin);
freopen("./output.txt","w",stdout);
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int T;
cin>>T;
while(T--) {
solve();
}
return 0;
}C.Digital Logarithm
Problem Description
Given two arrays, you can make one number in A/B array to become the length of number in 10-base(e.g. length of 88 is 2, 100 is 3). Two array is similar if you can change the order of the elements to make elements with same index equal. You are asked to give the minimum number of operations to make A&B equal.Solution
It’s clear that we can always make two arrays equal. They will all become to 1 anyway. It’s clear that if the biggest element in A and B are not equal, me must apply the operation on it, or we can’t make it similar. So, our solution is to use two heaps, every time we check the maximum element of two arrays and if they are equal, pop both of them(Of course!). Or, apply the operation on the bigger one.Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
using namespace std;
using ll = long long;
int getlen(int num) {
string str = to_string(num);
return str.length();
}
void solve() {
int n;
cin>>n;
vector<int> a(n), b(n);
priority_queue<int> pq1, pq2;
for(int i = 0; i < n;i++) {
cin>>a[i];
pq1.push(a[i]);
}
for(int i = 0; i < n; i++) {
cin>>b[i];
pq2.push(b[i]);
}
int ans = 0;
while(!pq1.empty()&&!pq2.empty()) {
int x = pq1.top(), y = pq2.top();
if(x==y) {
pq1.pop(), pq2.pop();
} else if(x>y) {
pq1.pop();
pq1.push(getlen(x));
ans++;
} else {
pq2.pop();
pq2.push(getlen(y));
ans++;
}
}
cout<<ans<<endl;
}
int main(){
freopen("./input.txt","r",stdin);
freopen("./output.txt","w",stdout);
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int T;
cin>>T;
while(T--) {
solve();
}
return 0;
}D. Letter Picking
Problem Description
Given a string and two players A and B. Every turn Alice/Bob pick the letter on the left/right of string and prepends to their string until the string is empty. The player with the smaller lexicographically win.Solution