CodeForces - 1710B Rain(前缀和+几何)

Posted on | In ,

比赛中没有想到解法。在浏览其他人代码时，发现许多选手使用了相同的思路，似乎是一种广为人知的解法，特此记录一下。

思路

按照题意可知，每个坐标x的雨将会形成一个坐标为xi, 高度pi的三角形，如下图。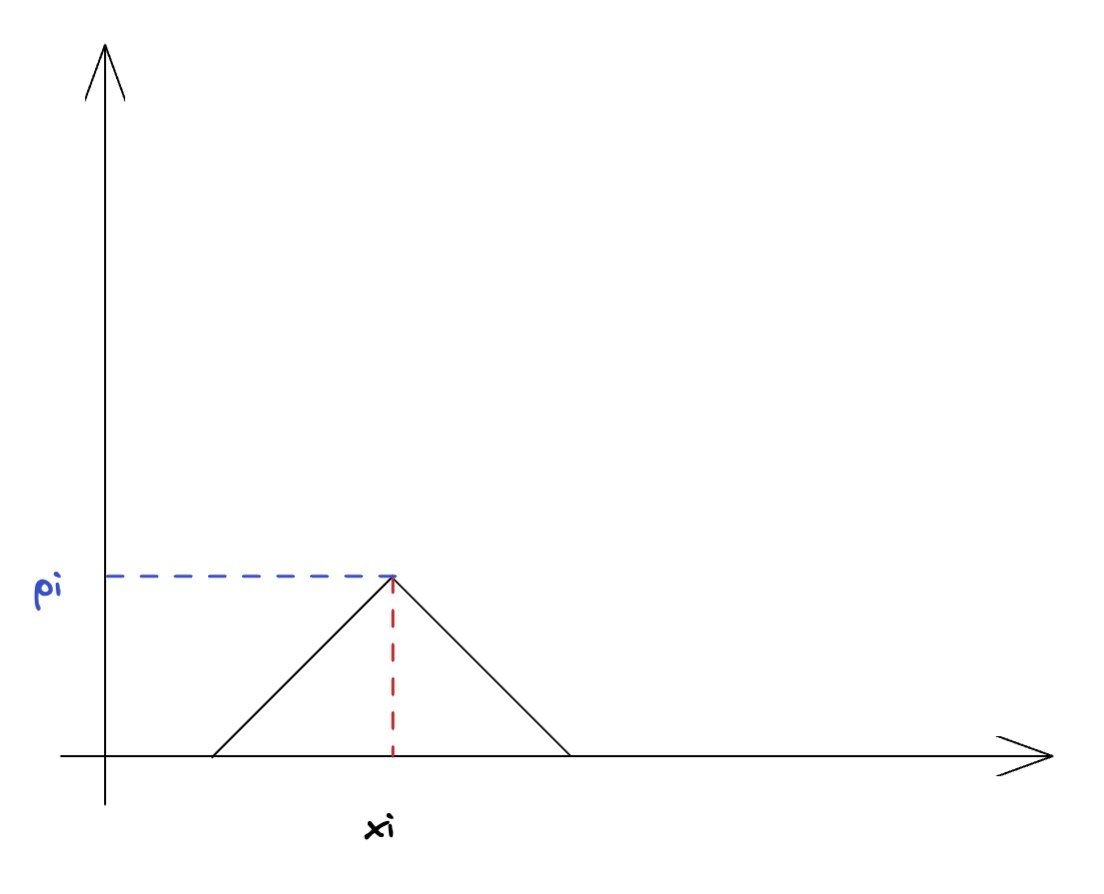
cf1710b-1.jpg
显然我们能发现，最高点一定是出现在雨的坐标xi上。那么首先就是如何计算每一个xi的高度。虽然一个雨的情况比较好计算，但是多个雨的情况，我们应当如何计算呢？一个比较常规的方式是进行两次前缀和的计算。下面我们以一个雨的情况进行讨论

1
2
3
高度: 0  0  1  2  1  0  0<br>
差分:  0  1  1  -1 -1 0<br>
二阶差分:1  0  -2  0 1

可以注意到，在二阶差分下，我们只要在左端点+1，最高点-2， 右端点+1，就能还原差分数组和高度数组。对于数据范围不大的题，这样就能完美还原图。但是这题的差分范围来到了1e9，遍历1e9来还原差分数组是不能接受的。这里的处理有两种方法。第一种是tutorial的方式，从左到右访问离散化的各个点。注意到虽然从差分数组到原数组的遍历非常麻烦，但是斜率的变化仅在二阶差分不为0的点发生。也就是说，斜率的变化是O(n)的。这样我们就能避免1e9的遍历，而对于高度的变化，我们能够通过kx+b类似的方式从第一个点开始从左向右扫描，进而算出所有点高度。在这一步上，tutorial和jiangly等oi的做法不太一样。tutorial是从左往右，一个一个点进行扫描。而jiangly的做法如下图所示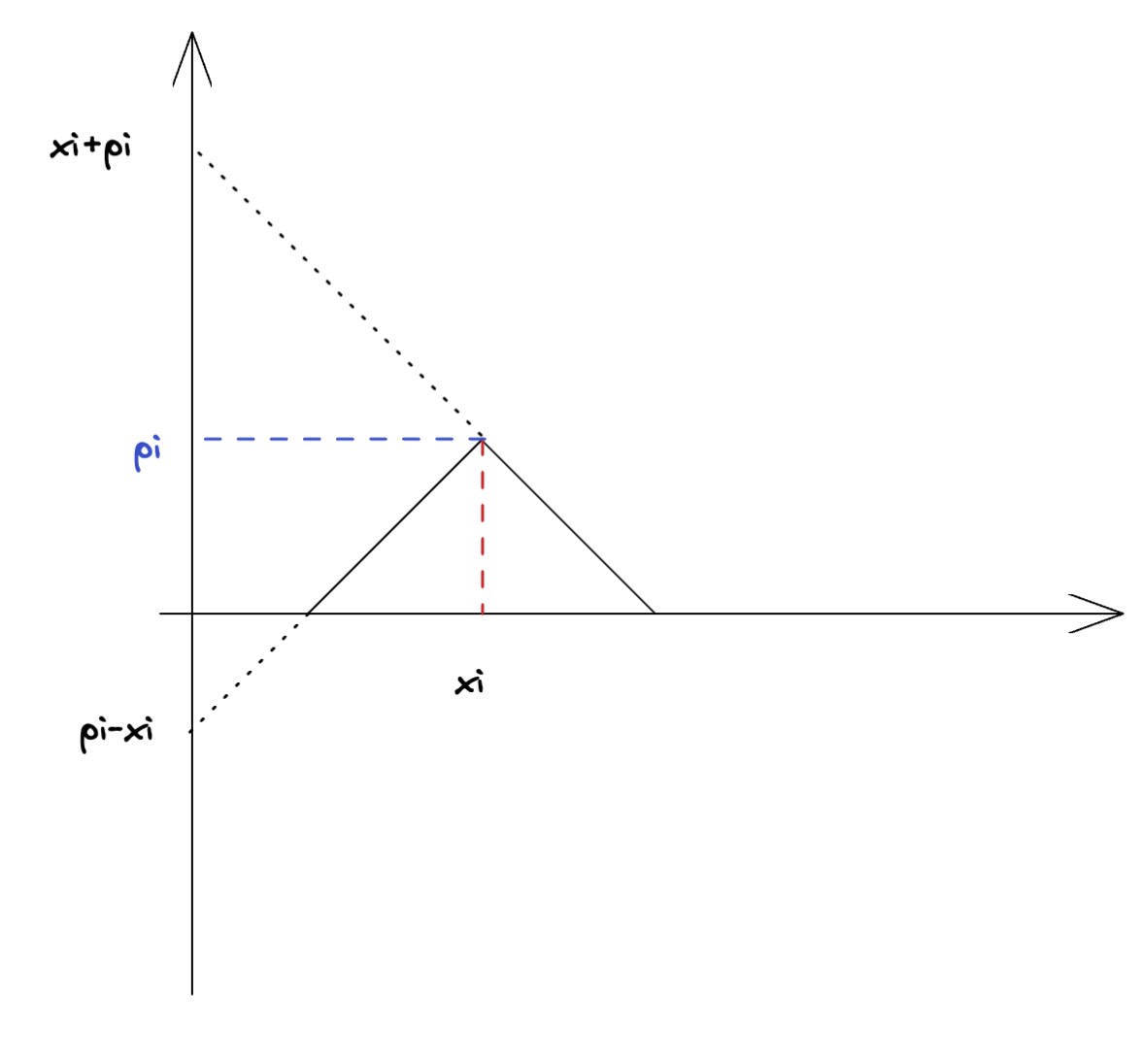
cf1710b-2.jpg
我看了很多选手都使用了这种做法。思路是对于这个三角形，延长两条边到y轴。那么截距就是pi-xi/pi+xi。然后我们将每个xi的截距相加作为每个雨对于xi点截距的贡献，参考代码中的value数组，最开始对l，j，r计算后，数组中保存的就是过xi直线的截距和。然后我们就只要考虑斜率对xi的影响了。这里只需要简单地用二阶差分计算即可。总体上来说，这种思路想要将所有雨对xi这个点的贡献，转化为一条直线表示。先计算截距贡献，再计算斜率（二阶差分转差分）。这似乎是一个非常通用的思路，思考过程和代码也非常简单。非常值得借鉴。

在解决了每个点高度的问题后，我们需要考虑，删除什么样的点，才能让大于m的点小于m。我们来看这样一张图：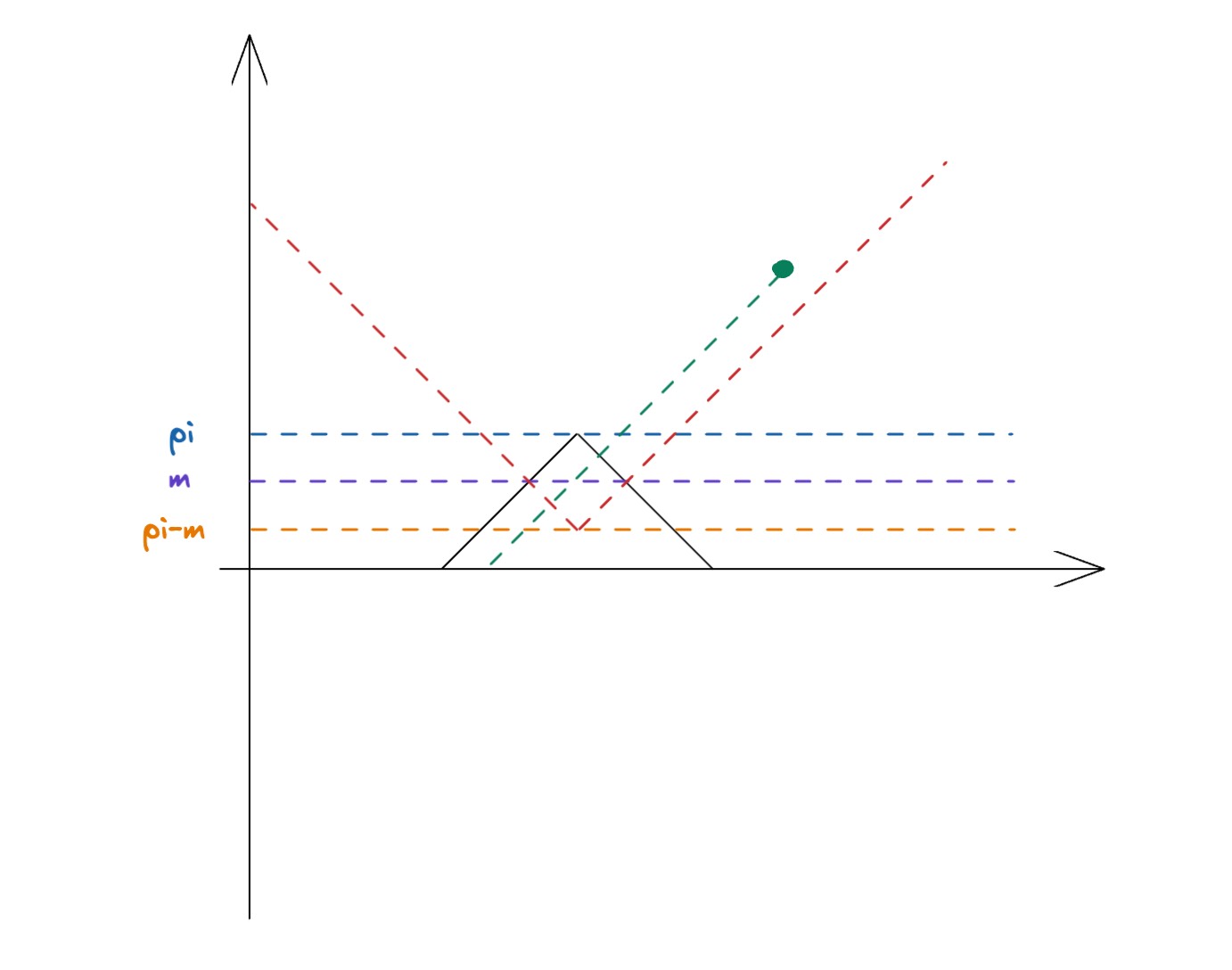
cf1710b-3.jpg
假定在xi我们有pi大于m。那么显然，当且仅当雨水点（注意是顶点）xj在红色虚线上方时，该雨水的贡献是大于pi-m的（如图中的绿色点）。所以移走xj是可以让xi变成小于m的状态。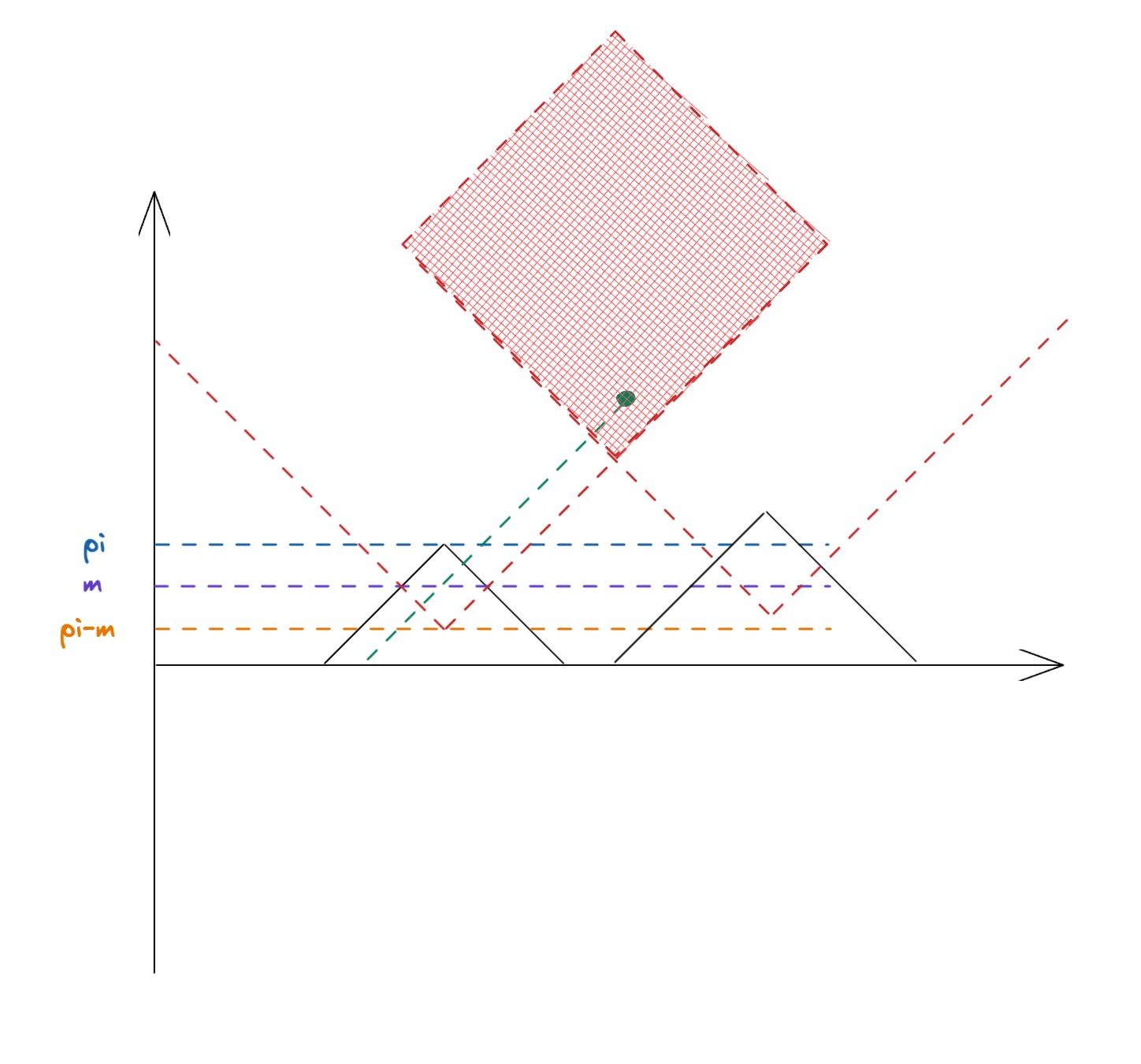
cf1710b-4.jpg
推广到多个雨水的场景，那么显然一次性能够让所有雨水小于m的点就是这种形状的交集，也就是上图中的红色区域（画板中没有类似的工具，但相信还是比较好理解的）。那么问题就是如何计算红色区域。这里tutorial和jiangly的做法又有所不同。tutorial的代码非常令人迷惑，思路如下：
cf1710b-5.jpg
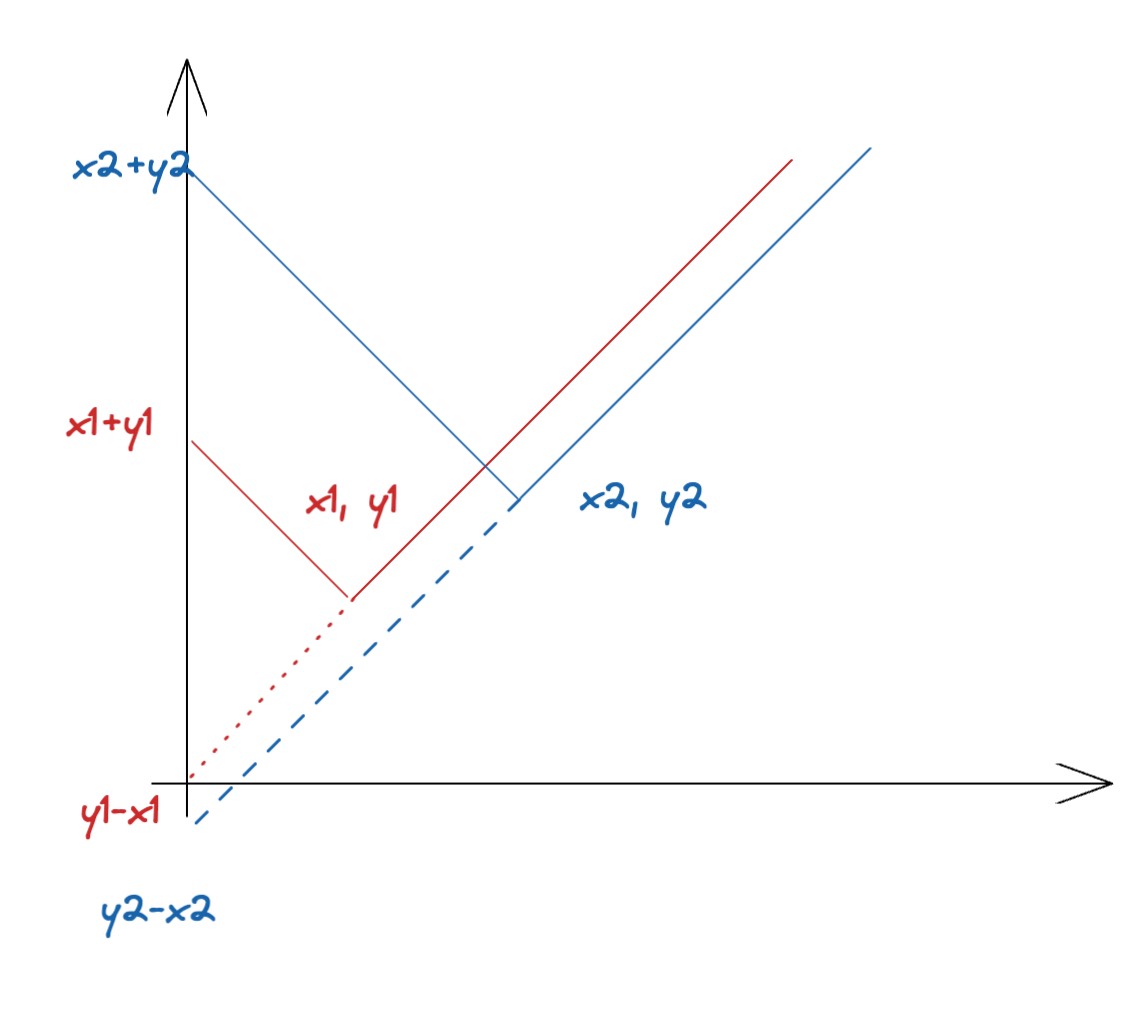
cf1710b-6.jpg
通过上图，我们能够发现，决定哪一根直线在上的，是它的截距。同时斜率的组合一定是k为-1和k为1的两根直线。所以我们只要将两个斜率的直线，分别求出斜率的最大值，就能找到处于交集，或者说上方的两根直线的截距。在知道截距后，显然能够通过一些比较简单的计算获取到交点的坐标（代入方程计算，这里不展开）。这种方法非常方便，但是第一眼看到这道题时不容易得到。

jiangly使用的则是另外一种思路：对所有直线分两类：斜率为1和斜率为-1。我们现在用斜率为1的进行讨论，斜率为-1的思路非常类似。首先，我们令dp[i]为满足对所有横坐标小于i的点能够被删除需要满足点的最小高度。我们是知道每个雨的高度的，在之前差分的过程中已经计算过了。此刻我们初始化所有点对dp的贡献。对于高度小于m的点，我们直接设高度为-inf，作用是在计算中让其不产生贡献。对高度大于m的，我们设高度为pi-m，可以理解为上图中的y1为pi-m。然后我们从左往右扫描。当扫到上图中的x2时，我们能看到，原先在x1的高度pi-m此时应该是pi-m+x2-x1。这时我们将其与y2比较并取最大值。如果x2高度本来就小于m，那么-inf显然不会有贡献。从左往右计算完后，再从右往左计算k=-1的dp数组。这样两者的最大值就是在i点，高于dpi的高度即可让所有点不泛洪。这个思路非常简单明了，不需要额外的思考。是一个非常方便的思路，也非常直观。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()

using namespace std;
using ll = long long;
ll gcd(ll a,ll b){
    return a%b==0?b:gcd(b,a%b);
}
ll quickpow(ll a,ll b,ll mod){ll ans=1ll;while(b){if(b&1ll)ans=(ans*a)%mod;a=a*a%mod,b>>=1;}return ans;}
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
int randint(int l, int r) { int out = rng() % (r - l + 1) + l; return out >= l ? out : out + r - l + 1; }
//head

void solve() {
    ll n, m;
    cin>>n>>m;
    vector<ll> x(n), p(n);
    for(int i = 0; i < n; i++) {
        cin>>x[i]>>p[i];
    }
    auto v = x;
    sort(all(v));
    v.erase(unique(all(v)), v.end());
    vector<ll> value(n), diff2(n);
    int c = v.size();
    for(int i = 0; i < n; i++) {
        int l = lower_bound(all(v), x[i]-p[i])-v.begin();
        int j = lower_bound(all(v), x[i])-v.begin();
        int r = lower_bound(all(v), x[i] + p[i]) - v.begin();
        value[l]+=(p[i]-x[i]);
        value[j]-=(p[i]-x[i]);
        value[j]+=(x[i]+p[i]);
        if (r < c) {
            value[r]-=(x[i]+p[i]);
        }
        diff2[l] += 1;
        diff2[j] -= 2;
        if ( r < c ) {
            diff2[r] += 1;
        }
    }
    for ( int i = 1; i < c; i++ ) {
        diff2[i] += diff2[i-1];
        value[i] += value[i-1];
    }
    for ( int i = 0; i < c; i++ ) {
        value[i] += diff2[i] * v[i];
    }
    bool nice = true;
    for ( int i = 0; i < c; i++ ) {
        if ( value[i] <= m ) {
            value[i] = -1e18;
        } else {
            value[i] -= m;
            nice = false;
        }
    }
    if ( nice ) {
        cout<<string(n, '1')<<endl;
        return;
    }
    auto pre = value, suf = value;
    for ( int i = 1; i < c; i++ ) {
        pre[i] = max(pre[i], pre[i-1]+v[i]-v[i-1]);
    }
    for ( int i = c-2; i >= 0; i-- ) {
        suf[i] = max(suf[i], suf[i+1]+v[i+1]-v[i]);
    }
    string ans;
    for ( int i = 0; i < n; i++ ) {
        int j = lower_bound(all(v), x[i]) - v.begin();
        ans += p[i] >= max(pre[j], suf[j])?'1':'0';
    }
    cout<<ans<<endl;
    
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("./input.txt","r",stdin);
    freopen("./output.txt","w",stdout);
#endif // ONLINE_JUDGE
    int T;
    cin>>T;
    while(T--) {
        solve();
    }
    return 0;
}