Aizu - 1313 Intersection of Two Prisms(辛普森积分)

思路

首先由题意，我们有一个平行于z轴的棱柱和一个平行于y轴的棱柱。想要通过三维几何运算来获得体积的方式显然是比较困难的。但我们注意到我们已经有的是两个保证底面为凸多边形的棱柱。这样有什么好处？我们考虑找一个垂直于x轴的平面，沿着平面对着这两个棱柱砍一刀会得到什么。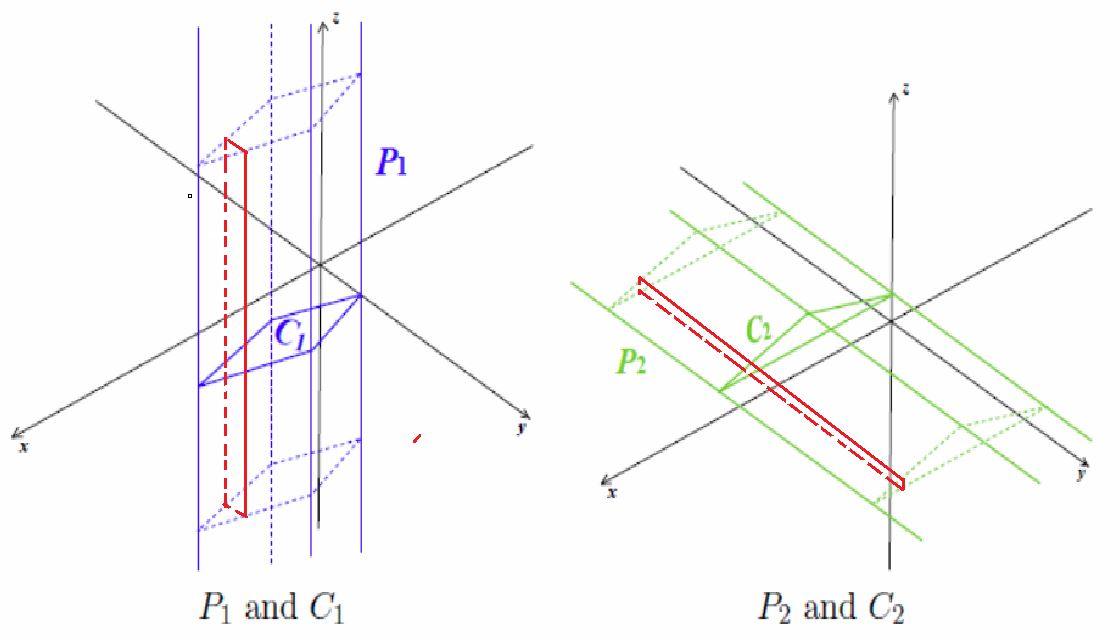

是两个长方形对不对？那么这两个长方形的交是什么？（注意，这时候我们砍的x是一样的）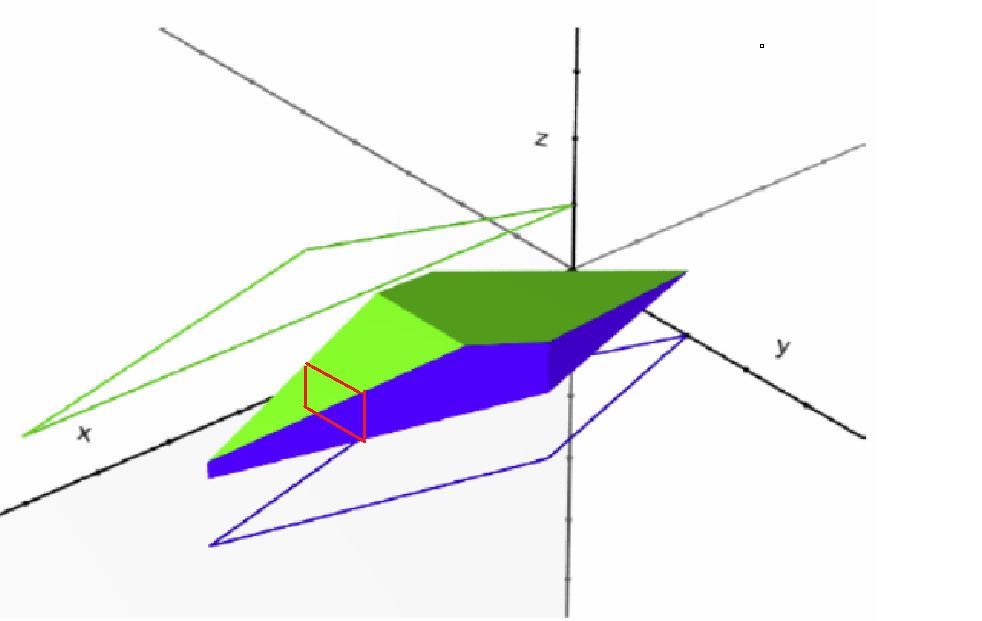

依然是一个长方形！而且显然在两个棱柱交的地方，对于每一个x砍一刀都有一个长方形。注意题意“两个保证底面为凸多边形的棱柱”，这是导致了当前情况的关键，凸多边形使得不会出现下图的情况：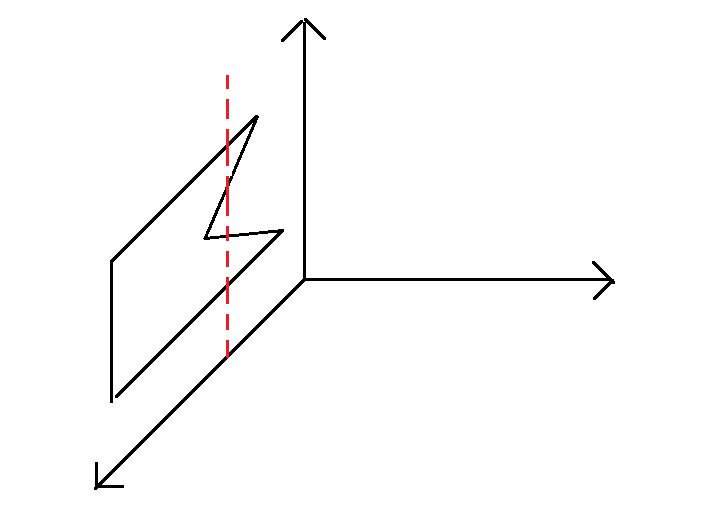

这样砍出来就不是长方形了，不过题目说了是凸多边形，所以不会出现上述情况。
那么现在我们要使用辛普森积分了。辛普森积分是形如下图的公式：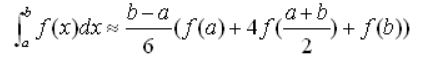

证明见关于辛普森积分法的研究。作为一个咸鱼选手当然只想知道板子怎么用。首先是辛普森积分在什么条件下使用：当我们的积分函数是二次及以下时，辛普森积分能够保证较高的精度。接下来是实际的使用：本题中我们首先将第一个多边形的x和第二个多边形的x全部取出存入一个vector，为什么要这么做？因为在这些x两两之间最后交出来的长方形的边长都是同一线性变化的，或者你看图，理解为我们切割时碰到了x的段点，这个时候长方形之后的边长虽然还是线性变化，却已经不是之前的变化函数了所以需要重新计算。而对于边长同一线性变化的区间，或者说两个相邻的x，我们就能使用辛普森积分进行计算。辛普森积分需要的是左端点(x1),右端点(x2),左端点函数值(fa,即在x1点我们切割两个棱柱得到的长度相乘。我们直接枚举棱柱的边求交，然后找y最大值-y最小值就是长度(z同理)，表现为代码中的width)，右段点（同理），中点（同理），有了这些函数值后我们就能获得面积沿x的积分，也就是这段的体积，最后我们逐段体积相加即可。

代码

#include <bits/stdc++.h>
#define ll long long
#define INF 0x7fffffff
#define inf 0x7fffffffffffffff
#define ms(a,val) memset(a,val,sizeof(a))
#define all(x) (x).begin(),(x).end()
#define sqr(x) ((x)*(x))
#define lowbit(x) ((x)&(-x))
ll quickpow(ll a,ll b,ll MOD){ll ans=1;while(b){if(b&1)ans=(ans*a)%MOD;a=a*a%MOD,b>>=1;}return ans;}
ll gcd(ll a,ll b){return a%b==0?b:gcd(b,a%b);}
using namespace std;
//head
//#define LOCAL

const int MAXN=150;
double X1[MAXN],Y1[MAXN];
double X2[MAXN],Z2[MAXN];

double getMin(double *a,int n){
    double mins=1e12;
    for(int i=0;i<n;i++)mins=min(mins,a[i]);
    return mins;
}
double getMax(double *a,int n){
    double maxs=-1e12;
    for(int i=0;i<n;i++)maxs=max(maxs,a[i]);
    return maxs;
}
//Remember the problem makes sure that it's a convex plogyen
double width(double *X,double *Y,int n,double x){
    double down=1e12,up=-1e12;
    for(int i=0;i<n;i++){
        double x1=X[i],y1=Y[i],x2=X[(i+1)%n],y2=Y[(i+1)%n];
        if(x1!=x2&&(x1-x)*(x2-x)<=0){
            double y=y1+(y2-y1)*(x-x1)/(x2-x1);
            down=min(down,y);
            up=max(up,y);
        }
    }
    return max(0.0,up-down);
}

int main(){
    #ifdef LOCAL
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    #endif // LOCAL
    int m,n;
    while(~scanf("%d%d",&m,&n)){
        if(!m&&!n)break;
        double res=0;
        for(int i=0;i<m;i++)scanf("%lf%lf",&X1[i],&Y1[i]);
        for(int i=0;i<n;i++)scanf("%lf%lf",&X2[i],&Z2[i]);
        int min1=getMin(X1,m),max1=getMax(X1,m),min2=getMin(X2,n),max2=getMax(X2,n);
        vector<int> xs;
        for(int i=0;i<m;i++)xs.push_back(X1[i]);
        for(int i=0;i<n;i++)xs.push_back(X2[i]);
        sort(all(xs));
        for(int i=0;i<xs.size()-1;i++){
            double a=xs[i],b=xs[i+1],c=(a+b)/2;
            if(min1<=c&&c<=max1&&min2<=c&&c<=max2){
                double functiona=width(X1,Y1,m,a)*width(X2,Z2,n,a);
                double functionb=width(X1,Y1,m,b)*width(X2,Z2,n,b);
                double functionc=width(X1,Y1,m,c)*width(X2,Z2,n,c);
                res+=(b-a)/6.0*(functiona+4*functionc+functionb);
            }
        }
        printf("%.10f\n",res);
    }
    return 0;
}