CodeForces - 956D Contact ATC(树状数组)

Posted on | In ,

思路

对于该题，我们建立如下图所示坐标系，横坐标为风速，纵坐标为在该风速下飞机到达0点的时间。那么显然在两条直线有交点的时候表示两架飞机同时到达0点。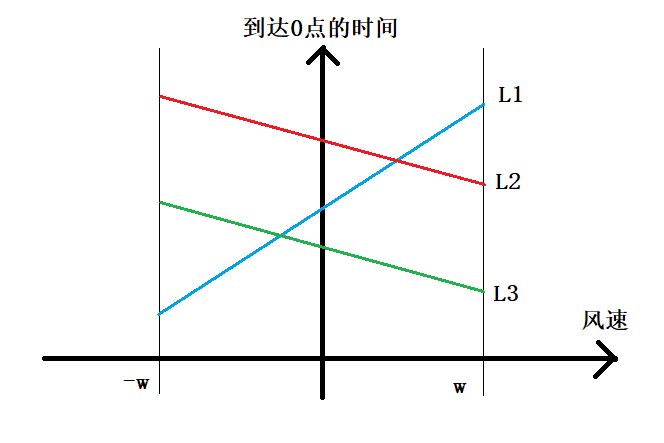
cf956d
虽然知道了这点，但我们不能O(n^2)求直线交，该题期望的是O(nlogn)的解法。在看了杜老师(%%%)的代码后我学到了一种新的姿势：已知多条直线在两个坐标x1,x2(这道题是-w，w)的情况下，我们可以使用树状数组求逆序对的方式来计算直线的交点数量。以本题为例：我们首先定义一个结构体，储存x(坐标的绝对值),v’(考虑风速后的速度),e(通过该值在左端点一样的情况下能够比较右端点),id。我们将-w各个点的值保存在一个vector up中，w保存在另一个vector down中，然后对两个数组根据到零点时间从小到大排序。对每个点我们利用id记录up（左端点）的左边排名，然后对右端点从上往下计算，每次我们查看在该点左端点之前排名的（也就右端点在它上面，左端点在它下面的直线）有几条，利用树状数组来维护这个值即可，最后的和就是我们需要的答案。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>
#define ll long long
#define INF 0x7fffffff
#define inf 0x7fffffffffffffff
#define ms(a,val) memset((a),(val),(sizeof(a)))
#define sqr(x) ((x)*(x))
#define all(x) (x).begin(),(x).end()
using namespace std;
ll quickpow(ll a,ll b,ll MOD){ll ans=1;a%=MOD;while(b){if(b&1)ans=ans*a%MOD;a=a*a%MOD,b>>=1;}return ans;}
ll gcd(ll a,ll b){return a%b==0?b:gcd(b,a%b);}
//head

const int MAXN=100005;
struct frac{
    ll p,q,e,id;
    frac(){};
    frac(ll p,ll q,ll e,ll id):p(p),q(q),e(e),id(id){};
    bool operator <(const frac &b)const{
        if(p*b.q!=b.p*q){
            return p*b.q<b.p*q;
        }
        else{
            //x smaller
            return p*b.e<b.p*e;
        }
    }
};
vector<frac> up,down;
ll BIT[MAXN],rk[MAXN];
#define lowbit(x) ((x)&(-x))
void add(int pos,ll val){
    int x=pos;
    while(x<MAXN){
        BIT[x]+=val;
        x+=lowbit(x);
    }
}
ll sum(int pos){
    int x=pos;
    ll sum=0;
    while(x>0){
        sum+=BIT[x];
        x-=lowbit(x);
    }
    return sum;
}

int main(){
    ll n,w,x,v;
    while(cin>>n>>w){
        for(int i=0;i<n;i++){
            cin>>x>>v;
            if(v<0){
                up.push_back(frac(x,-v+w,1,i));
                down.push_back(frac(x,-v-w,-1,i));
            }
            else{
                up.push_back(frac(-x,v-w,-1,i));
                down.push_back(frac(-x,v+w,1,i));
            }
        }
        sort(all(up));
        sort(all(down));
        ll ans=0;
        for(int i=0;i<n;i++)rk[up[i].id]=i+1;
        for(int i=n-1;i>=0;i--){
            ans+=sum(rk[down[i].id]);
            add(rk[down[i].id]+1,1);
        }
        cout<<ans<<endl;
    }
    return 0;
}