CodeForces Gym - 100959J Ropes(prufer序列)

Posted on | In ,

prufer序列学习笔记

prufer序列

prufer序列是一种标号无根树的表示方式（注意，标号需要从1-n两两不同）。我们通过这样一种方式生成一个prufer序列：首先找到无根树所有叶子节点中标号最小的节点，我们在prufer序列后插入它的相邻节点的标号，然后在树中删除这个节点。我们重复这个过程只到树中只剩两个节点。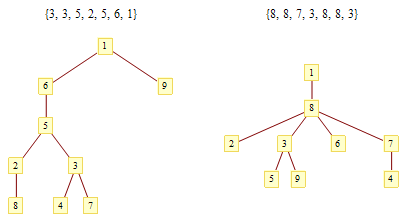
prufer-example
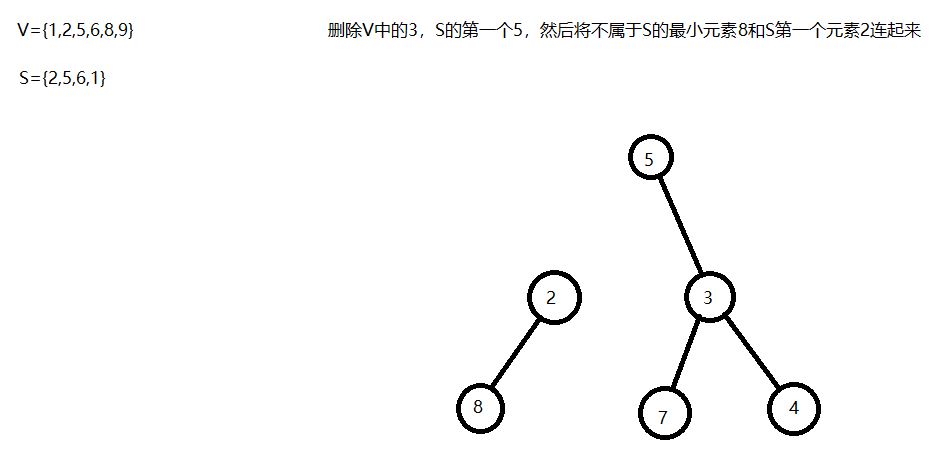
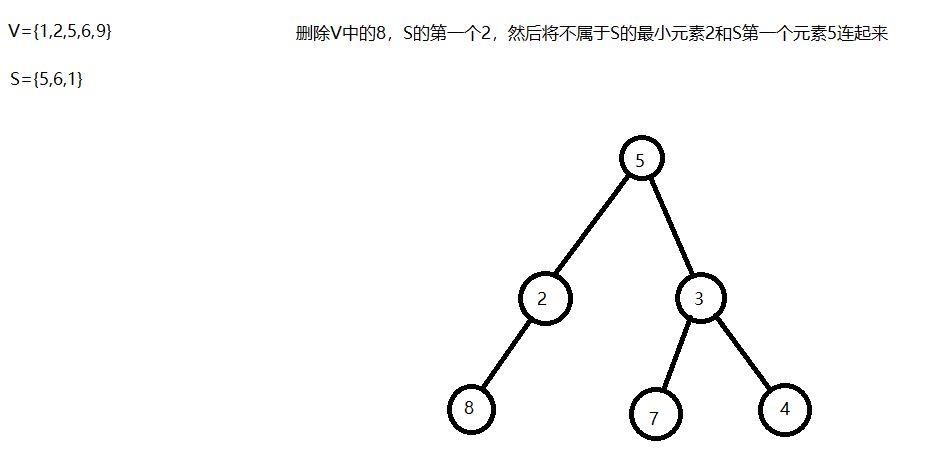
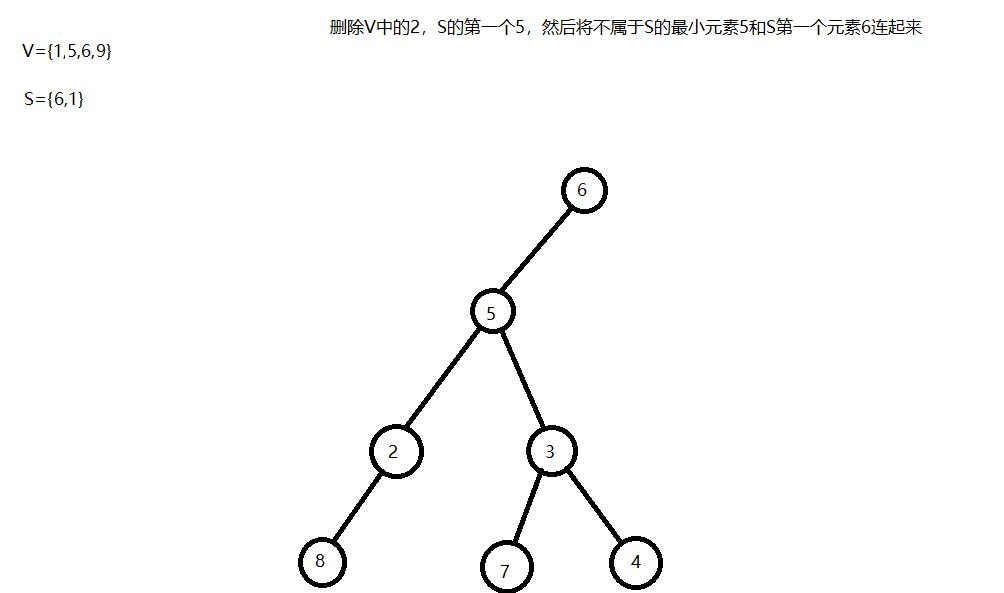
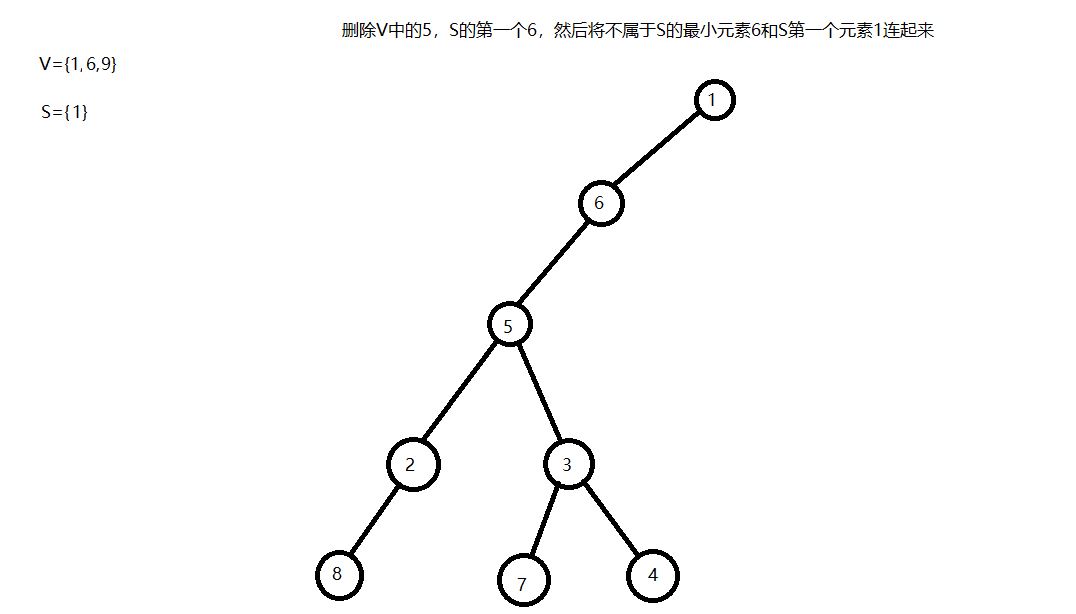
通过matrix67博客里的这张图我们能够更深地理解prufer序列是如何生成的。prufer序列有一个很有趣的性质，那就是一个prufer序列唯一地对应了一颗无根树，详细证明见matrix67的博客。我这里想详细写写如何从prufer序列生成无根树，我个人感觉理解了这个过程就理解了为什么prufer序列唯一地对应了一颗无根树的这个性质。我们以上面第一张图的3，3，5，2，5，6，1为例。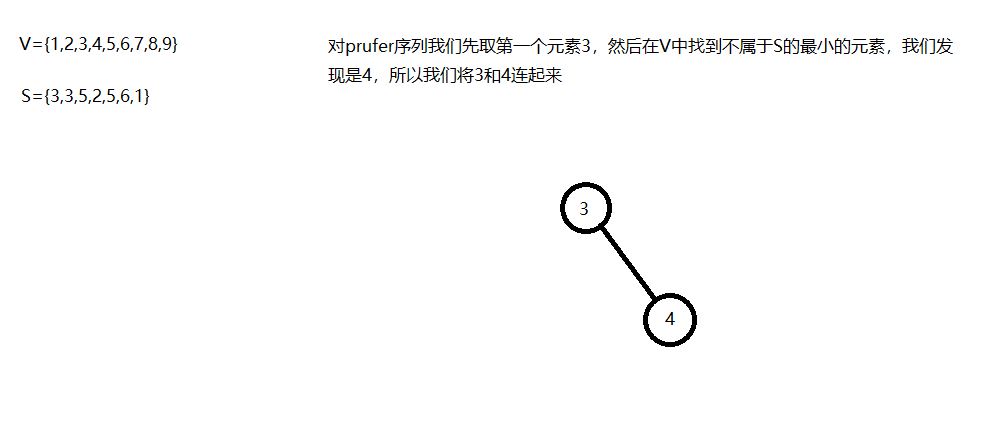
prufer_1
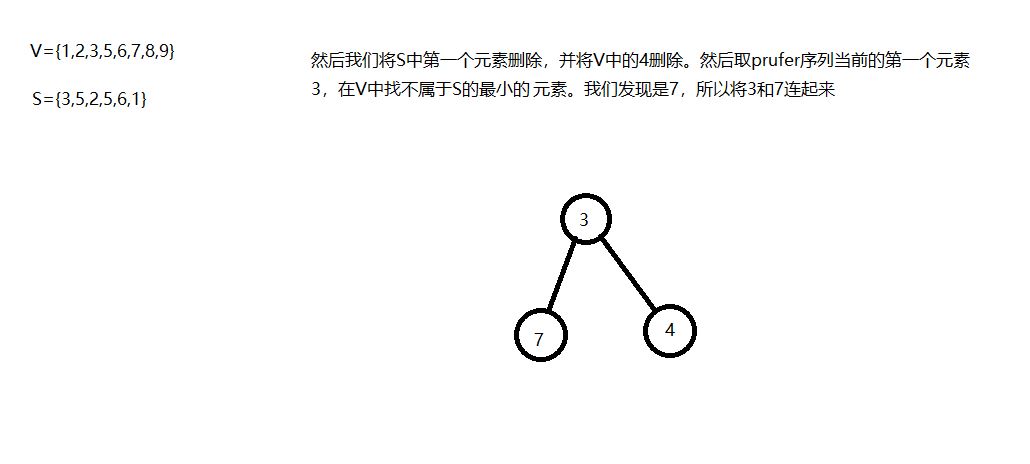
prufer_2
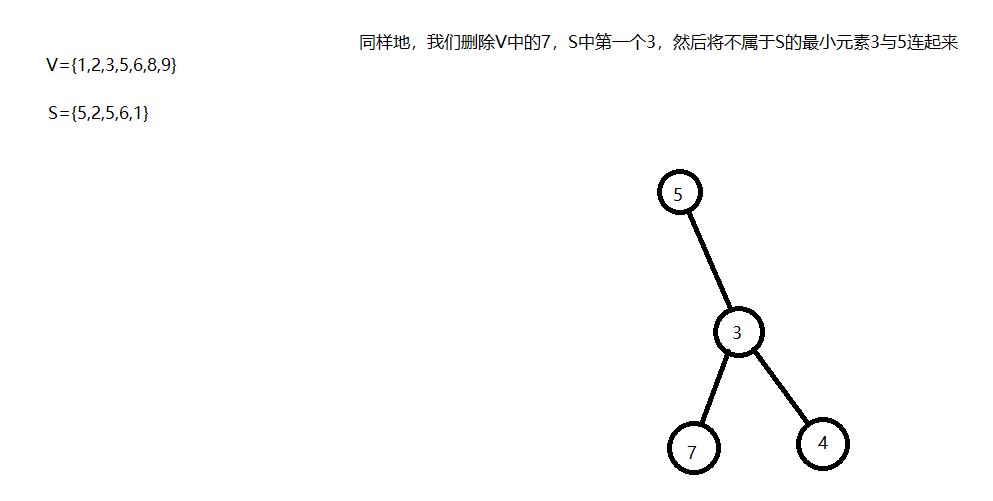
prufer_3
prufer_4
prufer_5
prufer_6
prufer_7
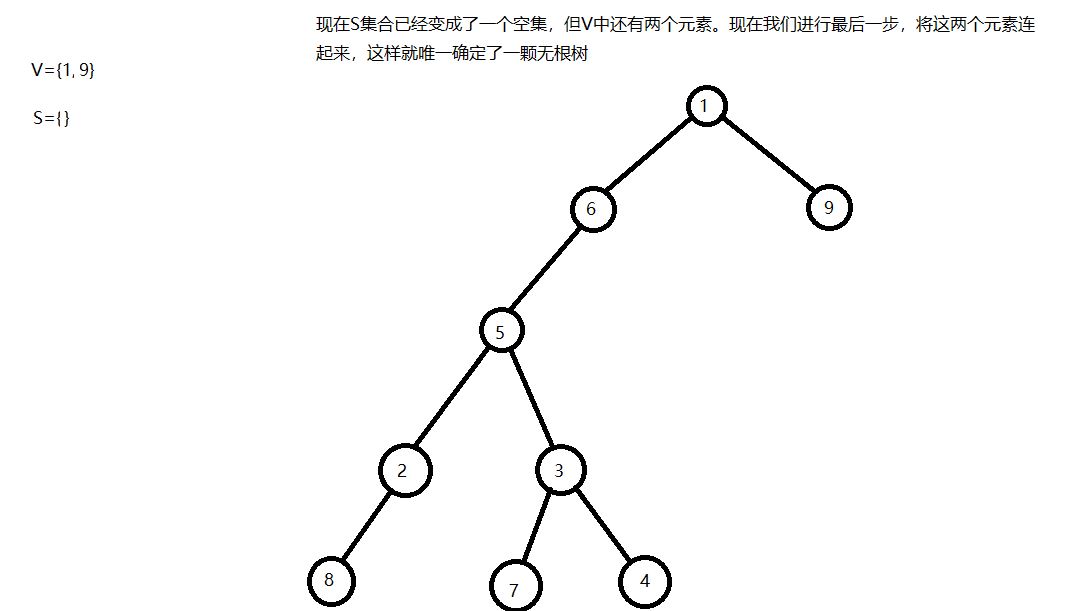
prufer_8

prufer序列的性质及推论

  1. prufer序列唯一地对应了一颗无根树
  2. prufer序列中，每个节点出现的次数等于它的度数减1
  3. n个点的无向完全图的生成树的计数：n^(n-2),即n个点的有标号无根树的计数。
  4. n个节点的度依次为D1, D2,…, Dn的无根树共有(n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]个，因为prufer唯一确定了一颗无根树，我们对序列进行全排列，同时Prufer编码中的数字i恰好出现Di-1次。

思路

裸的prufer序列题，注意判断无解

参考

经典证明：Prüfer编码与Cayley公式
树的计数 + prufer序列与Cayley公式 学习笔记

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
#define ll long long
#define INF 0x7fffffff
#define ms(a,val) memset((a),(val),(sizeof(a)))

using namespace std;

const ll MOD=1000000007;

int main() {
    ll n;
    while(~scanf("%I64d",&n)){
        ll ans=1,cnt=0,d,sum=0;
        for(ll i=0;i<n;i++){
            scanf("%I64d",&d);
            if(d==3)cnt++;
            sum+=(d-1);
        }
        if(sum!=n-2)printf("0\n");
        else{
            for(ll i=1;i<=n-2;i++){
                ll t=i;
                while(t%2==0&&cnt){
                    t/=2;
                    cnt--;
                }
                ans=ans*t%MOD;
            }
            printf("%I64d\n",ans);
        }
    }
	return 0;
}