HDU - 4089 Activation(概率dp)

Posted on | In , ,

思路

本题我们定义dp[i][j]为队伍中有i个人Tomato排在第j个时，服务器崩溃且排在他前面的人有大于等于k个人的概率。
一共有三个转移方程（注意是逆推）：

  1. dp[i][1]=p1*dp[i][1]+p2*dp[i][i]+p4，因为要求无后效性，化简可得dp[i][1]=p2/(1-p1)*dp[i][i]+p4/(1-p1)
  2. 对j属于[1,k]有：dp[i][j]=p1*dp[i][j]+p2*dp[i][j-1]+p3*dp[i-1][j-1]+p4，同样因为要求无后效性，化简可得dp[i][j]=p2/(1-p1)*dp[i][j-1]+p3/(1-p1)*dp[i-1][j-1]+p4/(1-p1)
  3. 对j属于[k+1,n]有:dp[i][j]=p1*dp[i][j]+p2*dp[i][j-1]+p3*dp[i-1][j-1]，化简可得dp[i][j]=p2/(1-p1)*dp[i][j-1]+p3/(1-p1)*dp[i-1][j-1]

接下来我们发现这个dp转移方程。。构成了一个环？不过这道题并没有用到高斯消元，我们将dp转移中第j项与dp[i]即当前状态无关的令为一个常数c[j]，然后对第一个方程迭代。我们最后化简可得如下式子：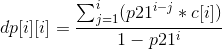
hdu4089
然后我们用转移方程求出所有dp[i]的状态，然后dp[n][m]就是答案。这题有个比较奇怪的点，似乎如果不对p4约等于0的情况进行特判会出问题？不是很懂为什么。。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
#define ll long long
#define INF 0x7fffffff
#define ms(a,val) memset((a),(val),(sizeof(a)))

using namespace std;

const int MAXN=2020;
const double eps=1e-5;
int n,m,k;
double p1,p2,p3,p4;
double dp[2][MAXN],c[MAXN],pp[MAXN];

int main() {
    while(~scanf("%d%d%d%lf%lf%lf%lf",&n,&m,&k,&p1,&p2,&p3,&p4)){
        double p21=p2/(1-p1),p31=p3/(1-p1),p41=p4/(1-p1);
        if(p4<eps){
            printf("0.00000\n");
            continue;
        }
        pp[0]=1.0;
        for(int i=1;i<MAXN;i++)pp[i]=pp[i-1]*p21;
        for(int i=1;i<=n;i++){
            c[1]=p41;
            for(int j=2;j<=k;j++)c[j]=p31*dp[(i-1)&1][j-1]+p41;
            for(int j=k+1;j<=n;j++)c[j]=p31*dp[(i-1)&1][j-1];
            double tmp=0;
            for(int j=1;j<=i;j++)tmp+=c[j]*pp[i-j];
            dp[i&1][i]=tmp/(1-pp[i]);
            dp[i&1][1]=p21*dp[i&1][i]+p41;
            for(int j=2;j<=n;j++)dp[i&1][j]=p21*dp[i&1][j-1]+c[j];
        }
        printf("%.5f\n",dp[n&1][m]);
        ms(dp,0);
    }
	return 0;
}