CodeForces Gym - 101615D Rainbow Roads(树上差分)

Posted on | In ,

思路

对于一个点，考虑可能出现同色边的情况，可以分为两种
(1)两个儿子是相同颜色的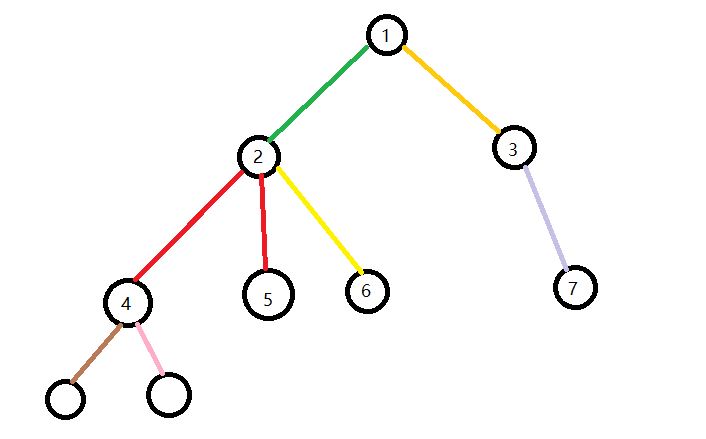
CodeForcesGym-101615D-1
如上图，显然2-4，2-5边是相同颜色的，同时对于4，5节点的子树上的点都不是good的，因为显然会有一条从5（4）到该点的一条不是rainbow road的路径。所以我们需要对这样的子树进行染色。
(2)父亲和儿子是相同颜色的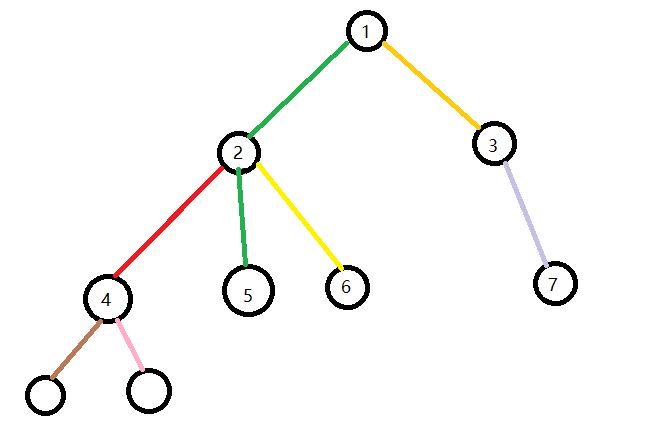
CodeForcesGym-101615D-2
这种情况下我们需要将除2和2的子树以外的所有节点进行染色。因为他们总有一条过1-2-5非彩虹路，所以那些节点不是good的。
现在我们解决了如何找出非good点这个问题，但是统计依然是大问题。我们需要对子树进行染色。我们注意到我们只需要最后输出一次答案即可而不需要一直回答询问，所以我们可以考虑树上差分。我们首先求出一个dfs序，得到st[i]和ed[i],对于第一种情况，因为st[i]和ed[i]之间的节点就是i和i的子树，我们使用差分即可。对于第二种情况，我们在根上+1，然后在子树上抵消这个+1即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <bits/stdc++.h>
#define ll long long
#define INF 0x7fffffff
#define ms(a,val) memset((a),(val),(sizeof(a)))

using namespace std;

const int MAXN=200010;
int head[MAXN],color[MAXN],to[MAXN],nxt[MAXN],cnt;
int st[MAXN],ed[MAXN],dfn,f[MAXN],sum[MAXN];
pair<int,int> q[MAXN];
void add(int u,int v,int w){
    to[cnt]=v;
    color[cnt]=w;
    nxt[cnt]=head[u];
    head[u]=cnt++;
}
void dfs(int u,int fa){
    st[u]=++dfn;
    f[u]=fa;
    for(int i=head[u];~i;i=nxt[i]){
        if(to[i]!=fa)dfs(to[i],u);
    }
    ed[u]=dfn;
}

int main() {
    int n;
    while(~scanf("%d",&n)){
        cnt=0,dfn=0;
        ms(head,-1),ms(sum,0);
        int u,v,w;
        for(int i=0;i<n-1;i++){
            scanf("%d%d%d",&u,&v,&w);
            add(u,v,w),add(v,u,w);
        }
        dfs(1,0);
        for(int i=1;i<=n;i++){
            int m=0;
            for(int j=head[i];~j;j=nxt[j])q[m++]=make_pair(color[j],to[j]);
            sort(q,q+m);
            int j=0,k=0;
            for(j=0;j<m;j=k){
                for(k=j;k<m&&q[j].first==q[k].first;k++);
                if(k>j+1){
                    for(int x=j;x<k;x++){
                        int y=q[x].second;
                        if(y==f[i]){
                            sum[1]++;
                            sum[st[i]]--;
                            sum[ed[i]+1]++;
                        }
                        else{
                            sum[st[y]]++;
                            sum[ed[y]+1]--;
                        }
                    }
                }
            }
        }
        for(int i=1;i<=n;i++)sum[i]+=sum[i-1];
        int ans=0;
        for(int i=1;i<=n;i++)if(!sum[st[i]])ans++;
        printf("%d\n",ans);
        for(int i=1;i<=n;i++)if(!sum[st[i]])printf("%d\n",i);
    }
	return 0;
}