BZOJ - 2301 Problem b(莫比乌斯反演+容斥)

Posted on | In ,

思路

莫比乌斯反演入门题，看popoqqq的ppt看了好久（本篇博客也是参考了很多他的ppt，然后加上了一些自己的理解），深深感到OI大佬的厉害Orz。

莫比乌斯反演

引子

首先我们考虑这样一个函数：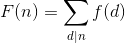
Mobius-function-1
由F(n)的定义，我们可以得到诸如
F(1)=f(1)
F(2)=f(1)+f(2)
F(3)=f(1)+f(3)
F(4)=f(1)+f(2)+f(4)
F(5)=f(1)+f(5)
F(6)=f(1)+f(2)+f(3)+f(6)
的式子。从而我们能从F(n)推得f(n)
f(1)=F(1)
f(2)=F(2)-F(1)
f(3)=F(3)-F(1)
f(4)=F(4)-F(2)
f(5)=F(5)-F(1)
f(6)=F(6)-F(3)-F(2)+F(1)
然后一位大牛从这个式子里看出了个规律：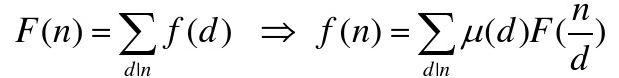
Mobius-function-2
其中μ(d)为莫比乌斯函数，这就是莫比乌斯反演公式，正确性的证明见popoqqq的ppt

莫比乌斯函数

莫比乌斯函数μ(d)的定义为:

  1. d=1,μ(d)=1
  2. d=p1*p2*…*pk为互异素数（互不相同的素数），那么μ(d)=(-1)^k
  3. 其他情况μ(d)=0

莫比乌斯函数的性质

  1. 当n=1时，μ(d)的前缀和为1，否则为0，证明见popoqqq的ppt
  2. 莫比乌斯函数是积性函数，所以我们可以使用线性筛来得到莫比乌斯函数（使用定义的第二条）

什么情况适合使用莫比乌斯反演

如果对一个函数f(n)，我们没法直接求出他的值，但我们能够求出他的约束和F(n)或者倍数和，那么我们就可以考虑莫比乌斯反演。接下来我们用bzoj2301来解释如何使用莫比乌斯反演。

思路

因为直接求这个询问非常麻烦，我们使用容斥原理将一个询问拆成4个，定义一个cal(a,b,k)函数为x属于[1,a],y属于[1,b]时gcd(x,y)=k数对的个数。那么我们就能将这个询问拆分为cal(b,d,k)-cal(a-1,d,k)-cal(b,c-1,k)+cal(a-1,c-1,k)。那么接下来我们怎么构造莫比乌斯反演？题目问的是x属于[1,n],y属于[1,m],gcd(x,y)=k的数对的个数，我们把这个问题扩张为x属于[1,n],y属于[1,m],k|gcd(x,y)（可以认为gcd(x,y)是k的倍数）数对的个数。对于后一个问题我们可以考虑对n来说k的倍数有几个，即floor(n/k),对y进行同样的考虑，所以我们得到了F(k)的表达式为floor(n/k)*floor(m/k)。这里我们能看出什么？我们碰到类似的这种题，我们要尽可能把F(k)设置为一个能够轻松得到的函数，而一般来说k的倍数/约数都是比较容易能够求得的，同时得到的函数F(k)和f(k)的关系也符合莫比乌斯反演，所以碰到类似的题要是没有思路的话尝试下倍数和和约数和是一个不错的选择。那么接下来我们就得到了莫比乌斯反演公式：
Mobius-function-3
通过枚举k的倍数我们能够在O(n)中解决问题。但是考虑到询问有5w个，最后的复杂度O(n^2)是不能接受的。考虑优化
通过观察发现floor(n/d)这个式子，我们发现取值最多有2根号n个取值。那么对floor(n/d)*floor(m/d)我们有2（根号n+根号m）个取值。注意这里不是两者相乘。为什么？我们考虑在d变化过程中n/d和m/d变化的过程。借用《POI XIV Stage.1 Queries Zap 解题报告》中的图：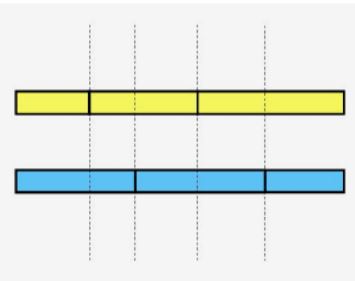
Mobius-example-1
我们把横轴看成d，每个竖杠代表着值的改变。我想很显然地我们能感受到为什么这个二元组只有2（根号n+根号m）个取值。所以我们枚举取值，并对莫比乌斯函数求一个前缀和，就能在O(sqrt(n))的时间内得到答案。

1
2
3
4
5
6
7
8
9
int cal(int a,int b,int k){
    a/=k,b/=k;
    int t=min(a,b),ans=0,last;
    for(int i=1;i<=t;i=last+1){
        last=min(a/(a/i),b/(b/i));
        ans+=(a/i)*(b/i)*(sum[last]-sum[i-1]);
    }
    return ans;
}

以上是枚举取值的代码。第五行是为了找出两个比值结果中的较小值。我个人理解实际上不除k的话似乎不会影响算法的正确性？似乎只是为了减少枚举的次数？我也不是很确定，如果有大佬知道的话望周知，谢谢！

参考

  • 莫比乌斯反演 - By popoqqq
  • BZOJ2301: [HAOI2011]Problem b[莫比乌斯反演 容斥原理]【学习笔记】

    代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    #include <bits/stdc++.h>
    #define ms(a,val) memset(a,val,sizeof(a))
    #define ll long long
    #define INF 0x7fffffff

    using namespace std;

    const int MAXN=50005;
    int cnt=0;
    int mobi[MAXN],vis[MAXN],prime[MAXN],sum[MAXN];
    void prework(){
        mobi[1]=1;
        for(int i=2;i<MAXN;i++){
            if(!vis[i]){
                prime[cnt++]=i;
                mobi[i]=-1;
            }
            for(int j=0;j<cnt&&i*prime[j]<MAXN;j++){
                vis[i*prime[j]]=1;
                //if there exists more than one same prime number, the value of the function is 0.
                if(i%prime[j]==0){
                    mobi[i*prime[j]]=0;
                    break;
                }
                mobi[i*prime[j]]=-mobi[i];
            }
        }
        sum[1]=1;
        for(int i=2;i<MAXN;i++)sum[i]=sum[i-1]+mobi[i];
    }

    //cal(b,d,k)-cal(a-1,d)-cal(b,c-1,k)+cal(a-1,c-1,k)
    int cal(int a,int b,int k){
        a/=k,b/=k;
        int t=min(a,b),ans=0,last;
        for(int i=1;i<=t;i=last+1){
            last=min(a/(a/i),b/(b/i));
            ans+=(a/i)*(b/i)*(sum[last]-sum[i-1]);
        }
        return ans;
    }
    int solve(int a,int b,int c,int d,int k){
        return cal(b,d,k)-cal(a-1,d,k)-cal(b,c-1,k)+cal(a-1,c-1,k);
    }

    int main() {
        int t;
        int a,b,c,d,k;
        scanf("%d",&t);
        prework();
        while(t--){
            scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
            printf("%d\n",solve(a,b,c,d,k));
        }
    	return 0;
    }