HDU - 3853 LOOPS(概率dp)

Posted on | In , ,

思路

概率/期望dp。本题我们能通过全期望公式得到dp[i][j]=dp[i+1][j]*map[i][j][2]+dp[i][j+1]*map[i][j][1]+dp[i][j]*map[i][j][0]+2得到(2是消耗的能量）。由于dp要求无后效性，我们移项得到dp[i][j]=(dp[i+1][j]*map[i][j][2]+dp[i][j+1]*map[i][j][1]+2)/(1-map[i][j][0])。需要注意的是对于概率dp，我们通常正推，但期望dp我们通常反着推。就期望dp来说，正推最大的困难点在于一个点可能是直接转移过来的，但也有可能在原地停留后再转移，即转移概率需要另外计算，所以概率并不是简单的map[i][j][k]。对于本题来说正推计算后的公式实际上还能接受，但对像hdu4405这种题来说正推的转移太复杂了，所以我们考虑泛用性更好的反推。对于一个点X，显然有如下转移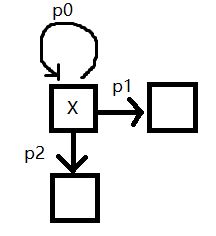
hdu-3853-1
那我们显然地，通过这个转移从起点到终点的期望等于使用这个转移从终点到起点的期望。对于这个反推我们考虑从右下往左上推，注意，这个时候每个点的期望是从右边的点，下面的点和自己推来的，这意味着原来正推的时候该点左下角的点对该点下面的点的影响是没有的，所以可以放心的使用全期望公式。
总结一下，我们使用反推通常是因为我们可以很方便地知道一个点到下一个点的转移概率，这个概率在反推的时候是不用额外计算的。但正推就要考虑之前的点有没有通过多种方式转移到这个点，我们需要考虑转移的概率究竟是几。两相比较之下显然反推比较优秀。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
#define ms(a,val) memset(a,val,sizeof(a))
#define ll long long
#define INF 0x7fffffff

using namespace std;

const int MAXN=1005;
double maps[MAXN][MAXN][3],dp[MAXN][MAXN];

int main() {
	int r,c;
	while(~scanf("%d%d",&r,&c)){
        ms(dp,0);
        for(int i=1;i<=r;i++){
            for(int j=1;j<=c;j++){
                for(int k=0;k<3;k++){
                    scanf("%lf",&maps[i][j][k]);
                }
            }
        }
        for(int i=r;i>0;i--){
            for(int j=c;j>0;j--){
                if(i==r&&j==c)continue;
                if(maps[i][j][0]==1.00)continue;
                dp[i][j]=(dp[i][j+1]*maps[i][j][1]+dp[i+1][j]*maps[i][j][2]+2)/(1-maps[i][j][0]);
            }
        }
        printf("%.3lf\n",dp[1][1]);
	}
	return 0;
}