学习一下主席树的使用
主席树
主席树是可持久化线段树的一种。应该可以看作是值域范围上的可持久化线段树?通常我们使用主席树解决区间第k大问题。
先考虑一个问题……
给定一个1e5大小的数组,多次询问l,r范围内第k大的数。
常规解法:离线后莫队
emmmm一切看起来很美好,速度也很快。那我们加一个条件:强制在线。
现在我们先考虑把问题弱化,如果问1-n上的第k大,要求在线,我们该怎么做?
权值线段树
为了解决上面这个问题,我们构造一棵权值线段树。每个叶子节点储存一个数字出现的次数(数字的范围可能要离散化),同时我们在每个节点上维护一个子节点数量。权值线段树的建树与线段树相同。查询第k大的时候,我们到一个节点观察其左儿子的子节点数量,如果大于等于k我们往左走,显然第k小数在左子树上,不然我们往右走,同时若子节点数量小于k显然在右子树,同时问题变成查右区间第(k-左子树子节点个数)大数。这样我们完美解决了这个弱化的问题。
回到主席树
那么现在的问题变成了怎么修改权值线段树让其支持区间第k大。我们考虑用一种类似“前缀和”的思想。一个常规的想法是我们先考虑建n(假定数组n个数)棵值域为1-m(假定我们已经处理好)的权值线段树,显然因为值域的预处理,我们能把它们放在一棵树上,然后节点上维护一个数组,表示第i次插入后节点的sum值,然后被询问l,r区间的时候,我们用把弱化问题中子节点数量变成sum[r]-sum[l-1](可以理解为变成了[l,r]区间的权值线段树),这样问题就转化为了上面的那个问题。但问题来了,这相当于建了n棵线段树,空间。。好像有点不够用啊?那我们现在观察一下,我们每次插入一个数x,那些节点修改了?显然只有从根到表示x的节点路径上的sum值发生了变化。所以我们考虑在插入的时候先新建一个根,然后复制前一个根给新建的根(为了链接左右儿子),然后就像我之前说的那样,只修改有影响的节点,没影响的指向之前树的节点(还是不理解的看下图)。通过对共同部分的利用,我们完成了节约空间的目的。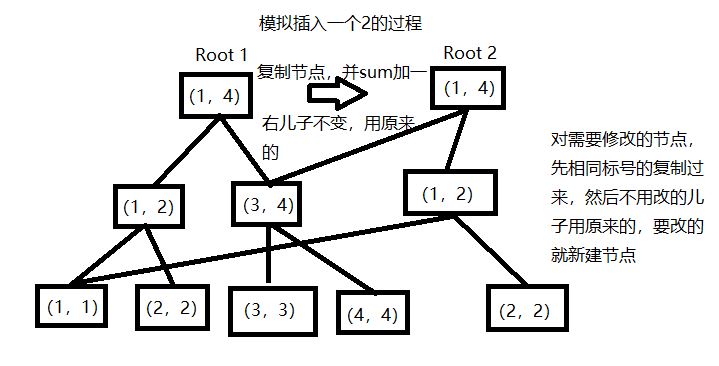
代码
1 |
|