HDU - 3948 The Number of Palindromes

Posted on | In , ,

思路

计算本质不同的回文串，回文树模板题

回文树

顾名思义，就是一个解决关于回文问题的数据结构，通常用来处理本质不同回文的个数。

回文树的元素

1.len[i]:i节点表示的回文串长度
2.next[i][c]:在i节点表示的回文串两边加c得到的回文串
3.fail[i]:当i失配后跳转不等于i表示的回文串自身的最长后缀回文
4.cnt[i]:节点i表示的本质不同的串的个数
5.num[i]:以节点i节点最右端点为回文串的结尾的回文串个数（需要在建完树后运行count）
6.last:上一个构建的回文串的位置
7.S[i]:第i次加入的字符S[0]=-1
8.p:添加的节点个数
9.n:添加的字符个数

回文树的构造

在参考中的《Palindromic Tree——回文树【处理一类回文串问题的强力工具】》详细讲解了回文树的构造方式，这里不再重复，主要讲讲我对回文树fail的理解。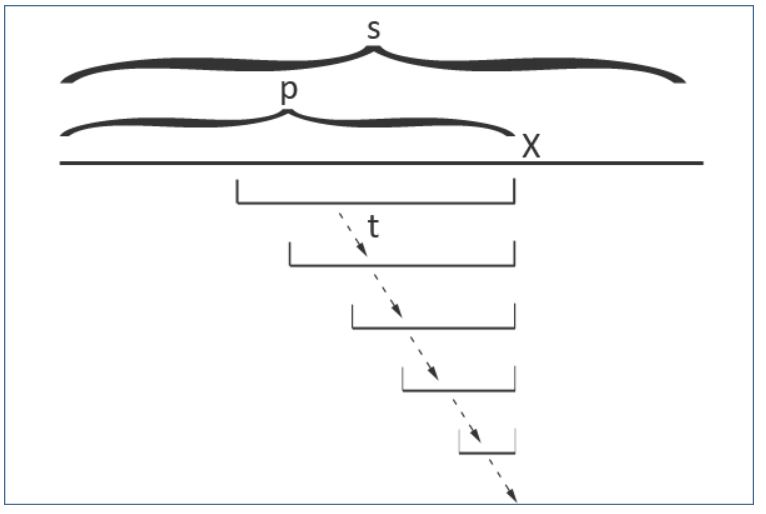
回文树的构造
当我们加入一个字符X时，如果我们希望XAX是一个回文串，那么A就必须是一个回文串，所以fail指针指向的就是在到结尾结束的回文串中更短的那个。如果A等于零，那么fail最终会指向长度为1的回文串，也就是我们想加入的字符X。这就是fail指针的意义。

回文树的应用

1.求串S前缀0~i内本质不同回文串的个数（两个串长度不同或者长度相同且至少有一个字符不同便是本质不同）(直接构造计算)
2.求串S内每一个本质不同回文串出现的次数（cnt[i])
3.求串S内回文串的个数（其实就是1和2结合起来）(p-2,也就是节点数-两个奇偶节点)
4.求以下标i结尾的回文串的个数（num[i])

参考

Palindromic Tree——回文树【处理一类回文串问题的强力工具】
回文树介绍(Palindromic Tree)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>
#define ll long long
#define INF 0x7fffffff
#define lson(x) (x<<1)
#define rson(x) ((x<<1)|1)
#define ms(a,val) memset((a),(val),(sizeof(a)))

using namespace std;

const int MAXN=100050;
const int N=26;
struct Palindromic_Tree {
    int nexts[MAXN][N],fail[MAXN],cnt[MAXN],num[MAXN],len[MAXN],S[MAXN],last,n,p;
    void init(string str){
        p=0;
        newnode(0);
        newnode(-1);
        last=0,n=0,
        S[n]=-1;
        fail[0]=1;
        for(int i=0;i<str.length();i++)add(str[i]);
    }
    int newnode(int length){
        for(int i=0;i<N;i++)nexts[p][i]=0;
        cnt[p]=0,num[p]=0,len[p]=length;
        return p++;
    }
    void add(int c){
        c-='a';
        S[++n]=c;
        int cur=getFail(last);
        if(!nexts[cur][c]){
            int now=newnode(len[cur]+2);
            fail[now]=nexts[getFail(fail[cur])][c];
            nexts[cur][c]=now;
            num[now]=num[fail[now]]+1;
        }
        last=nexts[cur][c];
        cnt[last]++;
    }
    int getFail(int x){
        while(S[n-len[x]-1]!=S[n])x=fail[x];
        return x;
    }
    void Count(){
        for(int i=p-1;i>=0;--i) cnt[fail[i]] += cnt[i] ;
    }
}pt;

int main() {
	int n;
	while(cin>>n){
        string str;
        for(int i=0;i<n;i++){
            cin>>str;
            pt.init(str);
            pt.Count();
            cout<<"Case #"<<i+1<<": "<<pt.p-2<<endl;
        }
	}
	return 0;
}