FFT模板题
FFT
快速傅里叶变换(FFT)是一种在O(nlog(n))时间内完成离散傅里叶变换的高效算法。在ACM中,我们通常用它加速多项式乘法。
一些预备知识
多项式的表示
对于常规的多项式,我们习惯使用系数表示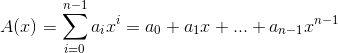
事实上,还有点值表示。我们通过将n个值带入一个n-1次多项式,通过x->f(x)的映射关系,我们也能唯一的表示一个多项式(考虑带入解方程组来还原)。
定理:一个n-1次多项式在n个不同点的取值唯一确定了该多项式。
系数表示和点值表示之间转换的时间表示的时间复杂度都是O(n^2)。(点值表示->系数表示可以用拉格朗日插值)
多项式的乘法
对于系数表示,我们算法的时间复杂度是O(n^2),这是显而易见的。而对于点值表示,我们会发现其多项式乘法的时间复杂度只有O(n)(显然我们只需要对两个多项式在同一个横坐标的地方的纵坐标相乘,我们就能得到A(x)*B(x)在这个点的纵坐标值)。由于点值表示的乘法时间复杂度只有O(n),所以我们要考虑的问题变成了如何快速将一个多项式的系数表示转换成点值表示。
FFT中要用到的复数知识
设a、b为实数,i^2=-1,形如a+bi的数叫做复数,其中i被称为虚数单位。复数域是已知最大的域。
该向量的长度a平方加b平方开根号叫做模长。从x轴正半轴到该向量的转角的有向(以逆时针为正方向)角叫做幅角。
复数相加满足的是平行四边形法则,复数相乘则是模长相乘,幅角相加。这个运算是要记住的,我们后面要用到。
对于朴素的插值算法,时间复杂度依然是O(n^2)。这制约了多项式乘法的时间复杂度。但实际上,我们可以通过巧妙地选取要带入的点,利用点的性质来加速乘法,我们要选取的点就是复数中的单位根。
单位根
下面的如果不特别指出,我们n默认取2的正整数次幂,因为hexo用Latex好麻烦(好吧其实是不会用TAT),下面令w(a,b)中a为上标,b为下标。
单位根指的是复平面上,以原点为圆心,1为半径作圆,然后把圆n等分,我们令辐角为0的w(0,n)为主n次单位根,其余的都是它的幂次。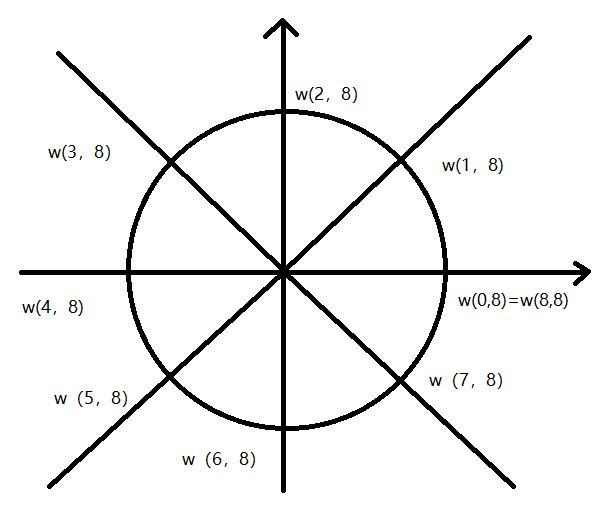
下面给出了单位根的一些性质
引理1(消去引理):对任何整数n>=0,k>=0,以及d>0我们有: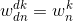
通过单位附属根的定义,利用复数的指数形式,这个引理很容易证明
引理2:对任意偶数n>0,有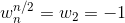
同样由定义易证
引理3(折半引理):如果n>0为偶数,那么n个n次单位复数根的平方的集合就是n/2个n/2次单位复数根的集合。
这个引理在下面证明的时候并不会使用,只是启发了我们下面式子将要使用的A(x^2)
证明:
对任意非负整数我们有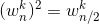
还有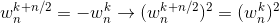
引理4(求和引理):对任意整数n>=1和不能被n整除的非负整数k,有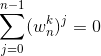
证明可用等比数列求和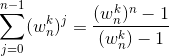
当且仅当k被n整除时,w(k,n)=1,且分母不为0.
以上就是FFT所需要的所有预备知识,大家只需要记住性质,因为后面证明要用到。
离散傅里叶变换
离散傅里叶变换就是将n个n次单位复数根代入多项式,求其点值表示。时间复杂度O(n^2)。
快速傅里叶变换
注意从这里开始n将是第一个大于两个多项式次幂的和的值,考虑我们一共需要两个多项式次幂的和才能插值,而且n要是2的整数次幂,因为在后面我们要使用奇偶分类,用2的整数次在后面会非常方便,在编程中体现在对n的处理和用0把两个多项式补到n次。虽然已经有较好的处理非2的整数幂的方法,但是混合基FFT比较麻烦,平时基本都是利用0补到2的整数次幂。
我们将多项式通过下标的奇偶分为两部分(虽然我不知道为什么会想到这么分,但这样分的确使得后面我们能分治加速dft):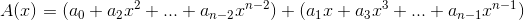
同时我们令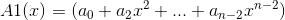
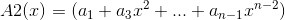
则有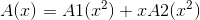
我们令k<n/2.
对于w(k,n)我们有: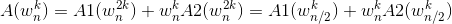
对于w(k+n/2,n)我们有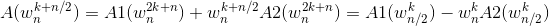
这里我们用到了w(n,n)=1和w(k+n/2,n)=-w(k,n)
通过上面的变换,我们能够发现当我们k取遍[0,n/2-1]时,k和k+n/2取遍了[0,n-1]。也就是说我们可以通过递归的解这个问题,通过把A1再视作之前的A,然后再做奇偶分类,直到数组长度为1再使用前面的式子合并子问题。时间复杂度为O(nlogn)。
以上就是FFT最常用的Cooley-Tukey算法。
傅里叶逆变换
虽然解决了从系数转换到点值,但反过来的复杂度依然是O(n^2)。而傅里叶逆变换就是为了解决这个问题。(这一部分我不是很明白下面的D是怎么得到的,所以大部分参考的Miskcoo’s Space中的文章。)
IDFT本质上就是解一个如下的线性方程组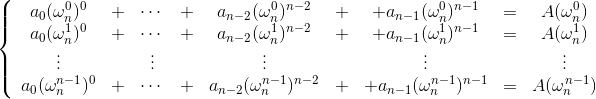
矩阵形式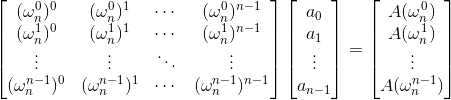
记上面的系数方程为V,考虑下面这个矩阵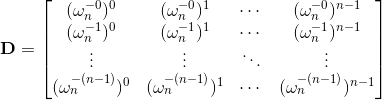
设相乘后的结果是E=DV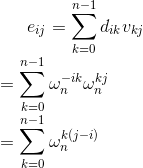
由引理4可知若i=j,eij=n
否则
因此可以知道In=E/n,所以 D/n=V的逆
如果在之前的矩阵方程进行左乘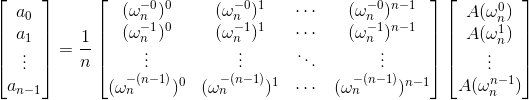
简单的说IDFT就是把DFT过程中使用单位根的倒数取代单位根,做一次fft再对每个数除n,就是傅里叶逆变换的结果。
傅里叶变换的迭代实现
使用递归实现的FFT常数和空间都比较大,所以我们使用两个方式进行优化。一个是二进制位翻转,另一个是蝴蝶操作。
二进制位翻转
我们模拟一次FFT分治的过程1
2
3
4
5
6000 001 010 011 100 101 110 111
0 1 2 3 4 5 6 7
0 2 4 6 - 1 3 5 7
0 4 - 2 6 - 1 5 - 3 7
0 - 4 - 2 - 6 - 1 - 5 - 3 - 7
000 100 010 110 001 101 011 111
我们发现,我们可以对每个数进行二进制位翻转,然后我们可以先2个2个合并,然后4个4个…这样就能使用迭代实现分治。
蝴蝶操作
在原来赋值的过程中,我们需要一个额外的b数组来存放数据,如下图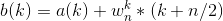
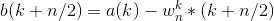
在处理完b后,最后统一放入a。这样实际上是非常浪费空间的。我们可以使用一个t保存w(k,n)*a(n/2+k),然后直接对a[k],a[k+n/2]操作,具体见代码
参考
算法导论第三十章 多项式与快速傅里叶变换
萌次的blogFFT 学习笔记
Miskcoo的blog从多项式乘法到快速傅里叶变换
本题思路
直接fft往上套就行,但最好数位翻转方便进位。不是很懂HDU?数组开小了怎么给的是WA啊。。
代码
有使用std::complex和自行实现complex,自行实现比较快(也就30ms..)
std::complex(时间265ms)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
using namespace std;
const double PI=acos(-1);
void fft(complex<double> *a, int n,complex<double> *com) {
int k = 0;
while ((1 << k)<n)k++;
for (int i = 0;i<n;i++) {
int t = 0;
for (int j = 0;j<k;j++)if (i&(1 << j))t |= (1 << (k - j - 1));
if (i<t)swap(a[i], a[t]);
}
for (int l = 2;l <= n;l *= 2) {
int m = l / 2;
for (complex<double> *p = a;p<a + n;p += l) {
for (int i = 0;i<m;i++) {
complex<double> t = com[n / l*i] * p[m + i];
p[m + i] = p[i] - t;
p[i]=p[i]+t;
}
}
}
}
complex<double> omega[140000], iomega[140000];
void init(int n) {
for (int i = 0;i<n;i++) {
omega[i] = complex<double>(cos(2 * PI / n*i), sin(2 * PI / n*i));
iomega[i] = conj(omega[i]);
}
}
void dft(complex<double> *a, int n) {
fft(a, n,omega);
}
void idft(complex<double> *a, int n) {
fft(a, n,iomega);
for (int i = 0;i<n;i++)a[i]/= n;
}
complex<double> a[140000], b[140000];
int ans[140000];
char s[50005];
int main() {
while (~scanf("%s", s)) {
ms(ans,0);
int len = strlen(s), n = 0;
for (int i = 0;i<50005;i++)a[i] = b[i] = complex<double>(0,0);
for (int i = 0;i<strlen(s);i++)a[strlen(s) - i - 1].real(s[i] - '0');
scanf("%s", s);
len += strlen(s);
for (int i = 0;i<strlen(s);i++)b[strlen(s) - i - 1].real(s[i] - '0');
while ((1 << n)<len)n++;
n = (1 << n);
init(n);
dft(a, n);
dft(b, n);
for (int i = 0;i<n;i++)a[i] =a[i]* b[i];
idft(a, n);
for (int i = 0;i<n;i++)ans[i] = (int)(a[i].real() + 0.5);
for (int i = 0;i<n;i++) {
ans[i + 1] += ans[i] / 10;
ans[i] = ans[i] % 10;
}
int cal = n;
while (!ans[cal]&&cal>0)cal--;
while (cal >= 0) {
printf("%d", ans[cal]);
cal--;
}
printf("\n");
}
return 0;
}
自行实现(时间234ms)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
using namespace std;
const double PI=acos(-1);
struct Complex{
double real,image;
Complex(){real=0,image=0;}
Complex(double real){this->real=real,image=0;}
Complex(double real,double image){this->real=real,this->image=image;}
Complex operator +(const Complex &c){
return Complex(c.real+real,c.image+image);
}
Complex operator -(const Complex &c){
return Complex(real-c.real,image-c.image);
}
Complex operator *(const Complex &c){
return Complex(c.real*real-c.image*image,c.real*image+c.image*real);
}
Complex operator *(double x){
return Complex(real*x,image*x);
}
Complex operator /(double x){
return Complex(real/x,image/x);
}
Complex rev(){
return Complex(real,-image);
}
};
void fft(Complex *a, int n,Complex *com) {
int k = 0;
while ((1 << k)<n)k++;
for (int i = 0;i<n;i++) {
int t = 0;
for (int j = 0;j<k;j++)if (i&(1 << j))t |= (1 << (k - j - 1));
if (i<t)swap(a[i], a[t]);
}
for (int l = 2;l <= n;l *= 2) {
int m = l / 2;
for (Complex *p = a;p<a + n;p += l) {
for (int i = 0;i<m;i++) {
Complex t = com[n / l*i] * p[m + i];
p[m + i] = p[i] - t;
p[i]=p[i]+t;
}
}
}
}
Complex omega[140000], iomega[140000];
void init(int n) {
for (int i = 0;i<n;i++) {
omega[i] = Complex(cos(2 * PI / n*i), sin(2 * PI / n*i));
iomega[i] = omega[i].rev();
}
}
void dft(Complex *a, int n) {
fft(a, n,omega);
}
void idft(Complex *a, int n) {
fft(a, n,iomega);
for (int i = 0;i<n;i++)a[i] =a[i]/ n;
}
Complex a[140000], b[140000];
int ans[140000];
char s[50005];
int main() {
while (~scanf("%s", s)) {
ms(ans,0);
int len = strlen(s), n = 0;
for (int i = 0;i<50005;i++)a[i] = b[i] = Complex();
for (int i = 0;i<strlen(s);i++)a[strlen(s) - i - 1].real=s[i] - '0';
scanf("%s", s);
len += strlen(s);
for (int i = 0;i<strlen(s);i++)b[strlen(s) - i - 1].real=s[i] - '0';
while ((1 << n)<len)n++;
n = (1 << n);
init(n);
dft(a, n);
dft(b, n);
for (int i = 0;i<n;i++)a[i] =a[i]* b[i];
idft(a, n);
for (int i = 0;i<n;i++)ans[i] = (int)(a[i].real + 0.5);
for (int i = 0;i<n;i++) {
ans[i + 1] += ans[i] / 10;
ans[i] = ans[i] % 10;
}
int cal = n;
while (!ans[cal]&&cal>0)cal--;
while (cal >= 0) {
printf("%d", ans[cal]);
cal--;
}
printf("\n");
}
return 0;
}