POJ - 1330 Nearest Common Ancestors(倍增LCA)

Posted on | In ,

思路

在有根树中，我们称距离u和v所有公共祖先中距离最近的称为最近公共祖先(LCA)。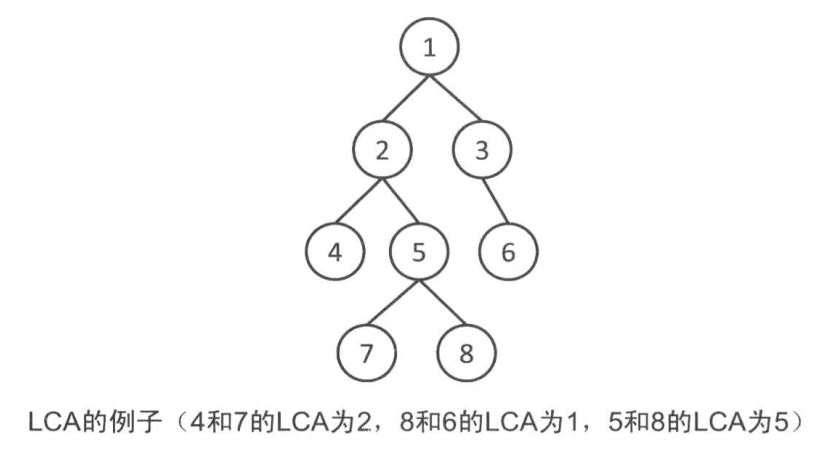
LCA
一个朴素的求u和v的LCA的想法是让u和v先深度相同，然后逐层向上直到碰到相同元素。复杂度为O(n)。虽然看着简单有效，但对多次查询来说这个复杂度十分不友好。
为了高效求解公共祖先，我们有三种方式：

  • 倍增法（在线，实现简单）
  • RMQ（在线，实现复杂）
  • Tarjan（离线）

本题我们使用倍增法求LCA。倍增法构造LCA预处理复杂度为O(nlogn),查询复杂度为O(logn)。
下面会涉及到的一些元素：

  • parent[k][v]:距离v元素2^k距离的祖先
  • depth[v]:v元素的深度

我们首先通过dfs(int v,int p,int d)初始化parent[0][v],depth[v],根的祖先为-1

1
2
3
4
5
6
7
void dfs(int v, int p, int d) {
	parents[0][v] = p;
	depth[v] = d;
	for (vector<int>::iterator it = G[v].begin();it != G[v].end();it++) {
		if(*it!=p)dfs(*it, v, d + 1);
	}
}

接着倍增初始化。外循环是倍增的k，内循环是节点，因为要先求出所有节点的parent[k][v]才能初始化k+1的情况（考虑parent[k+1][v]=parent[k][parent[k][v]])。
1
2
3
4
5
6
7
8
9
void init() {
	dfs(root, -1, 0);
	for (int k = 0;k + 1 < MAX_LOG_V;k++) {
		for (int v = 1;v <= n;v++) {
			if (parents[k][v] < 0)parents[k + 1][v] = -1;
			else parents[k + 1][v] = parents[k][parents[k][v]];
		}
	}
}

如果我们用朴素的方法，令数组parent[k][v]为v的k祖先的话预处理时间复杂度会达到O(n^2)，所以是不可接受的。而倍增的话我们在初始化后先将u，v放到同一高度，然后可以进行类似二分搜索的方式。从MAX_LOG_V - 1开始，如果parent[k][v]!=parent[k][u]，那么就向上倍增，这样能保证往上后的节点还没到最近公共祖先，有点类似十进制数贪心变成二进制数的方式。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int lca(int u, int v) {
	if (depth[u] > depth[v])swap(u, v);
	for (int k = 0;k < MAX_LOG_V;k++) {
		if (((depth[v] - depth[u]) >> k) & 1) {
			v = parents[k][v];
		}
	}
	if (u == v)return u;
	for (int k = MAX_LOG_V - 1;k >= 0;k--) {
		if (parents[k][u] != parents[k][v]) {
			u = parents[k][u];
			v = parents[k][v];
		}
	}
	return parents[0][u];
}

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
#include <functional>
#include <cmath>
#include <queue>
#include <vector>
#include <map>
#include <set>
#include <stack>
#include <cctype>
#include <sstream>
#define INF 1e9
#define ll long long
#define ull unsigned long long
#define ms(a,val) memset(a,val,sizeof(a))
#define lowbit(x) ((x)&(-x))
#define lson(x) (x<<1)
#define rson(x) (x<<1+1)

using namespace std;
int n;
const int MAXN = 10005, MAX_LOG_V = 20;
vector<int> G[MAXN];
int root,deg[MAXN],parents[MAX_LOG_V][MAXN],depth[MAXN];
void dfs(int v, int p, int d) {
	parents[0][v] = p;
	depth[v] = d;
	for (vector<int>::iterator it = G[v].begin();it != G[v].end();it++) {
		if(*it!=p)dfs(*it, v, d + 1);
	}
}
void init() {
	dfs(root, -1, 0);
	for (int k = 0;k + 1 < MAX_LOG_V;k++) {
		for (int v = 1;v <= n;v++) {
			if (parents[k][v] < 0)parents[k + 1][v] = -1;
			else parents[k + 1][v] = parents[k][parents[k][v]];
		}
	}
}
int lca(int u, int v) {
	if (depth[u] > depth[v])swap(u, v);
	for (int k = 0;k < MAX_LOG_V;k++) {
		if (((depth[v] - depth[u]) >> k) & 1) {
			v = parents[k][v];
		}
	}
	if (u == v)return u;
	for (int k = MAX_LOG_V - 1;k >= 0;k--) {
		if (parents[k][u] != parents[k][v]) {
			u = parents[k][u];
			v = parents[k][v];
		}
	}
	return parents[0][u];
}
int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int t,u,v;
	cin >> t;
	while (t--) {
		cin >> n;
		ms(deg, 0),ms(parents,0),ms(depth,0);
		for (int i = 0;i < n-1;i++) {
			cin >> u >> v;
			G[u].push_back(v);
			deg[v]++;
		}
		for (int i = 1;i <= n;i++) {
			if (deg[i] == 0) {
				root = i;
				break;
			}
		}
		init();
		cin >> u >> v;
		cout << lca(u, v) << "\n";
		for (int i = 0;i < MAXN;i++)G[i].clear();
	}
	return 0;
}