SPOJ - SUBST1 New Distinct Substrings

Posted on | In , ,

思路

题意是计算字符串所有本质不同的子串。主要思路是利用后缀数组的性质。因为是第一次使用后缀数组，所以在这里稍微做一些笔记。

后缀数组

后缀指的是从字符串的某个位置到字符串结尾的子串（包括原串和空串）。而后缀数组指的是包括所有字符串后缀的一个数组，同时其中的后缀已经完成了字典序的排序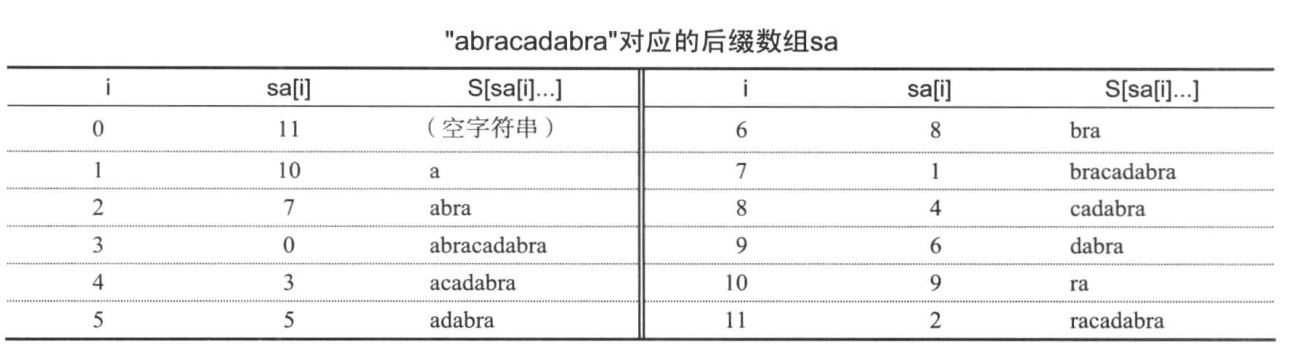
Suffix-Array
上图就是白书中后缀数组的样例，其中sa[i]指的是从第几个字符开始的后缀。

后缀数组的生成

在了解了后缀数组的内容后我们首先来讲讲如何实现。后缀数组的实现类似于基数排序，先比较各个后缀的第一个字符，然后利用这次的比较结果，我们能够计算长度为2的rank（先比较前一个长度为一的字符串，在比较后一个）。通过不断倍增长度最后完成对所有长度字符串的排序，如果发现后半部分长度超过字符串长度的话，就令他为最小的（-1）,可以参考下面第二张图的a的第二个rank。这里或许会不能理解为什么可以这样比，难道不会有遗漏的字符使得这样的比较不能够进行吗？答案是否定的。实际上每一个后缀的第一个字符拼在一起就是整个字符串，所以不用担心有缺漏的情况。这个过程的时间复杂度为O(nlog^2n)。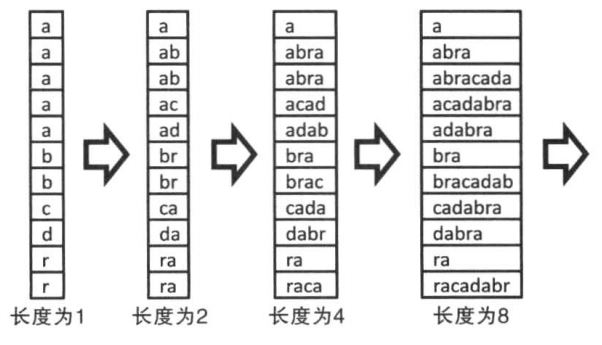
Suffix-Array-Sort1
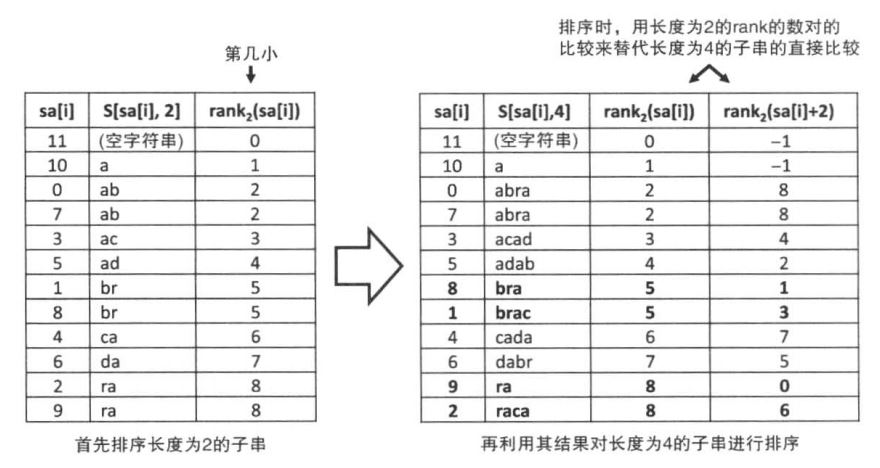
Suffix-Array-Sort2

高度数组

高度数组指的是相邻两个后缀的公共最长前缀。
Suffix-Array-Height-Array
在高度数组中，最关键的就是height[i] ≥ height[i - 1] - 1这个性质。i与i-1指的是sa中相邻的两个后缀，比如abra和bra，从上图中我们能够看到abra后面三个子串和bra后面三个子串只是差一个前面的a，那么我们就能复用之前abra的height数组，所以显然有height[i] ≥ height[i - 1] - 1，构造的时间复杂度为O(n)。

本题思路

在了解了后缀数组的性质后，我们可以发现，一个后缀对子串数量的贡献是str.length()-sa[i]-height[i]。原理是height就是重复的子串，减掉就是去重的过程。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
#include <cmath>
#include <queue>
#include <vector>
#include <set>
#include <stack>
#include <cctype>
#include <sstream>
#define INF 1e9
#define ll long long
#define ull unsigned long long
#define ms(a,val) memset(a,val,sizeof(a))
#define lowbit(x) ((x)&(-x))
#define lson(x) (x<<1)
#define rson(x) (x<<1+1)

using namespace std;
int n,k;
const int MAX_N=60000;
int ranks[MAX_N+1];
int tmp[MAX_N+1];

//倍增计算rank
bool compare_sa(int i,int j){
	if(ranks[i]!=ranks[j])return ranks[i]<ranks[j];
	else{
		int ri=i+k<=n?ranks[i+k]:-1;
		int rj=j+k<=n?ranks[j+k]:-1;
		return ri<rj;
	}
}
void construct_sa(char S[],int *sa){
	n=strlen(S);
	//对长度为1的字符直接使用ascii码,长度为0的后缀rank值为-1
	for(int i=0;i<=n;i++){
		sa[i]=i;
		ranks[i]=i<n?S[i]:-1;
	}
	for(k=1;k<=n;k*=2){
		sort(sa,sa+n+1,compare_sa);
		tmp[sa[0]]=0;
		for(int i=1;i<=n;i++){
			tmp[sa[i]]=tmp[sa[i-1]]+(compare_sa(sa[i-1],sa[i])?1:0);
		}
		for(int i=0;i<=n;i++){
			ranks[i]=tmp[i];
		}
	}
}
void construct_lcp(char S[],int *sa,int *lcp){
	int n=strlen(S);
	for(int i=0;i<=n;i++)ranks[sa[i]]=i;
	int h=0;
	lcp[0]=0;
	for(int i=0;i<n;i++){
		int j=sa[ranks[i]-1];
		if(h>0)h--;
		for(;j+h<n&&i+h<n;h++){
			if(S[j+h]!=S[i+h])break;
		}
		lcp[ranks[i]-1]=h;
	}
}
int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int t;
	char s[MAX_N+1];
	cin>>t;
	while(t--){
		int ans=0;
		int lcp[MAX_N+1],sa[MAX_N+1];
		ms(lcp,0),ms(sa,0),ms(ranks,0),ms(tmp,0);
		cin>>s;
		construct_sa(s,sa);
		construct_lcp(s,sa,lcp);
		int len=strlen(s);
		for(int i=1;i<=len;i++){
			ans+=len-sa[i]-lcp[i];
		}
		cout<<ans<<"\n";
	}
	return 0;
}