POJ – 2352 Stars

Posted on | In ,

思路：
说来惭愧，看到这道题的第一反应是一个二维的树状数组（因为题没读完）。在读二维树状数组的资料时恰好看到了别人的资料，发现读入数据是按照y坐标的递增序读入的。那么对于y的考虑显然是不必要的，所以只需要一维就能够完成这道题。这道题使用y递增序化二维问题为一维问题似乎是个不错的解题思路？然后由于是第一次手写BIT的板子，在这里稍微做一些笔记吧。

BIT
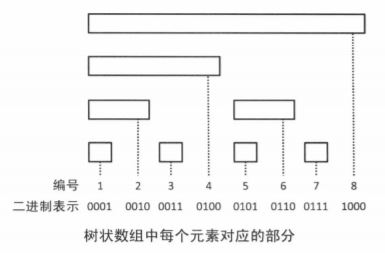
在白书上对于树状数组提供的功能有两个：
1.给定位置，计算前缀和

通过上图的二进制我们能够发现为了求到n的区间和，我们可以通过不断去掉末尾的1（即lowbit）然后对BIT[n]求和的方法来计算前缀和。那么怎么理解这个过程？我的理解是在建立树状数组的时候我们可以把每个部分看成一个小的树状数组。很显然应该能够理解类似100这样的二进制数在维护一个大区间，然后对于后面的两个0位，我们通过添加一个1（对于两个0位每添加一个1就是一个新区间，不能添加两个，不然就跑到7去了，可以对照着图理解）构成了一个小的树状数组的空间（101，110），通过这样不断递归的定义最终完成了整个树状数组。所以在回过头去求的时候我们就要去掉末尾的1返回到前面那个区间。
2.给定位置的变化量，更新维护的前缀和
根据上面的介绍，不难理解对于形如1xxx（x为0或者1）的数都处于一个类似小树状数组的空间中，通过左移1可以在同一个树状数组中逐层向上，所以而1xxx又处在10000（即多一位）的区间中，所以显然是可以这样更新的。

树状数组通常用来求解逆序对以及前缀和询问。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
#include <cmath>
#include <queue>
#include <vector>
#include <map>
#include <cctype>
#include <sstream>
#define INF 1e9
#define ll long long
#define ms(a,val) memset(a,val,sizeof(a))

#define lowbit(x) ((x)&(-x))

using namespace std;
int bit[35000],level[17000],n;
int sum(int pos) {
    int i=pos,ans=0;
    while (i > 0) {
        ans += bit[i];
        i -= lowbit(i);
    }
    return ans;
}
void add(int pos, int x) {
    int i = pos;
    while (i <= 35000) {
        bit[i] += x;
        i += lowbit(i);
    }
}
int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    while (cin>>n) {
        int x, y;
        ms(bit, 0),ms(level,0);
        for (int i = 0;i < n;i++) {
            cin >> x >> y;
            int lev = sum(x+1);
            level[lev]++;
            add(x+1, 1);
        }
        for (int i = 0;i < n;i++) cout << level[i] << "\n";
    }
    return 0;
}